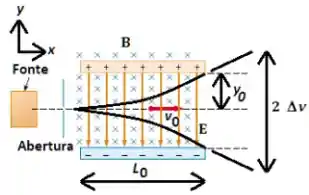
Q - A figura ao lado mostra um modelo do chamado filtro de velocidades. Nele, uma fonte de

partículas de massa e carga elétrica gera um feixe que é colimado por uma abertura. Esse feixe atravessa uma região do espaço que contém campos elétrico, , e magnético, , constantes e uniformes, de tal modo que apenas as cargas com determinado valor de velocidade , conseguem atravessar o filtro em trajetória retilínea e uniforme. A ideia do filtro de velocidades é que as cargas que tenham velocidades maiores ou menores que

irão se defletir por causa da ação dos campos elétrico e magnético e vão se chocar com as placas positiva ou negativa do sistema. Mas como a figura mostra (através de linhas curvas grossas), algumas cargas com velocidade , embora se defletam, não colidem com as placas e conseguem sair do filtro de velocidades. Se um anteparo for colocado próximo à saída do filtro de velocidades, ele mostrará uma mancha cuja largura vai corresponder a uma incerteza ou imprecisão, , da medida do filtro de velocidades. (Para facilitar os cálculos, considere que para as cargas que tenham e conseguem sair do filtro de velocidades, a força resultante sobre elas é apenas ao longo da direção e que é pequeno o suficiente de modo que a componente da velocidade na direção é , para obter um resultado aproximado).

Obtenha uma expressão para em função apenas das propriedades da partícula carregada, e , dos campos elétrico e/ou magnético, da velocidade e dos parâmetros geométricos do filtro de velocidades (ver na figura).

Supondo que você possa mudar os valores da intensidade dos campos elétrico e magnético, qual dos dois campos (ou os dois) você mudaria, e de quanto você os mudaria, para que diminua de 20% e a velocidade se mantenha a mesma? Explique.

A velocidade é que a partícula precisa ter para atravessar o filtro sem sofrer deflexão.

Para que ela não sofra deflexão a força elétrica deve ser igual a força magnética, e vamos conseguir tirar a velocidade disso já que a força magnética depende de , assim temos que:

Então essa é a velocidade para a partícula não sofrer deflexão.

Agora vamos atrás da velocidade , para achar essa velocidade podemos tanto considerar que a partícula foi mandada para cima como para baixo, já que o caminho que ela faz é o mesmo.

Vamos considerar que ela foi jogada para cima, assim temos que a força magnética é maior que a elétrica, gerando uma força resultante, assim temos que:

Com isso vamos usar a equação da posição para quando temos uma aceleração, assim temos:

Onde e que é a velocidade inicial na direção , não podemos esquecer que mesmo sendo a uma equação para a direção , a velocidade da partícula é a velocidade com que ela entra no filtro que é a na direção , assim temos que:

Então temos que saber o tempo que a partícula leva para atravessar o filtro.

Segundo o enunciado para facilitar as contas podemos considerar a velocidade na direção como sendo , então usando a equação da posição para um movimento sem aceleração temos:

Assim temos que:

Substituindo no que encontramos no passo anterior, temos:

Agora que temos e , vamos encontrar , assim temos que:

Agora vamos pensar no que o item pede. Ele quer saber como podemos mexer nas intensidades do campo afim de diminuir em , mas mantendo a mesma.

Primeiro, para manter a mesma com as mudanças nos campos, para isso temos que fazer a mesma mudança nos dois, já que:

Então temos que diminuir ou aumentar os campos com o mesmo fator para essa fração se mantenha igual. Agora para termos uma redução de , temos que:

Onde é a imprecisão com a redução dos vamos e é o que já tínhamos, assim:

Supondo que que mexemos em cada campo por um fator , assim:

Assim temos que:

Então temos que aumentar nossos campos para que tenhamos uma redução de de .

E com isso finalizamos a questão!