Um elétron é abandonado do repouso em uma região do espaço onde há um campo elétrico uniforme no plano da página, apontando para o topo da mesma, e um campo magnético uniforme apontando para fora do plano da página. Nessa situação, qual caminho na figura abaixo melhor descreve a trajetória inicial do elétron nessa região?
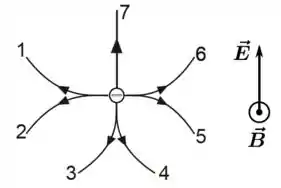
- 5
- 1
- 2
- 3
- 4
- 6
- 7
Passo 1
Para resolvermos essa questão, vamos colocar o sistema de referência como mostrado à esquerda na Figura abaixo. Dada essa referência, podemos escrever, respectivamente, os campos elétrico e magnético da seguinte maneira:
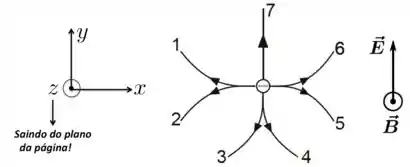
Como temos um campo elétrico apontando na direção do eixo , então a força elétrica sobre o elétrico será
Passo 2
Vamos olhar, agora, para a força magnética em cada uma das trajetórias indicadas.
A) Trajetórias 1 e 2 da Figura:
Em ambas trajetórias, o vetor velocidade inicial do elétron é . Por isso, a força magnética é dada por
onde é o produto vetorial entre os vetores unitários e . Substituindo esse produto vetorial na expressão acima para a força, temos
Portanto, a força magnética está ao longo do eixo . Agora, dá uma olhada na Figura acima e repara que, em ambas as trajetórias 1 e 2, existiria uma força atuando sobre o elétron que o puxaria para dentro da curva. Por isso, essa força deveria ter uma componente também na direção do eixo . Beleza?
Bom, como tanto a força elétrica como a força magnética estão na direção , podemos eliminar as trajetórias iniciais 1 e 2 como possíveis trajetórias para o elétron, já que as forças nesses casos teria uma componente também na direção do eixo .
Passo 3
B) Trajetórias 5 e 6 da Figura:
Agora, também em ambas as trajetórias, o vetor velocidade inicial do elétron é . Então, a força magnética nesse caso é dada por
onde é o produto vetorial entre os vetores unitários e . Substituindo esse produto vetorial na expressão acima para a força, temos
De novo, a força magnética, assim como a força elétrica, só tem componente na direção . Como essas são as duas únicas forças atuando sobre o elétron, as trajetórias 5 e 6 não são possíveis, já que não há componente na direção da força que puxa a carga para dentro da trajetória.
Passo 4
C) Trajetória 7 da Figura:
Aqui, o vetor velocidade inicial do elétron é . Então, a força magnética nesse caso é dada por
onde é o produto vetorial entre os vetores unitários e . Substituindo esse produto vetorial na expressão acima para a força, temos
Por essa razão, a trajetória inicial 7, que é retilínea apontando para o eixo , não é possível.
Passo 5
D) Trajetórias 3 e 4 da Figura:
Aqui, o vetor velocidade inicial do elétron é . Por isso, a força magnética é dada por
onde é o produto vetorial entre os vetores unitários e . Substituindo esse produto vetorial na expressão acima para a força, temos
Por essa razão, descartamos a trajetória 3 como possibilidade, já que a força atuando sobre o elétron nesse caso teria uma componente ao longo do eixo .
Resta, então, a trajetória 4. Nessa trajetória, só para a gente fechar a discussão completa de todos os casos, temos uma força que atua puxando o elétron para dentro da curva. Por isso, essa força deve ter uma componente apontando para o eixo , além da força elétrica .
Portanto, a trajetória inicial seguida pelo elétron é a de número 4.
Resposta
Letra e).