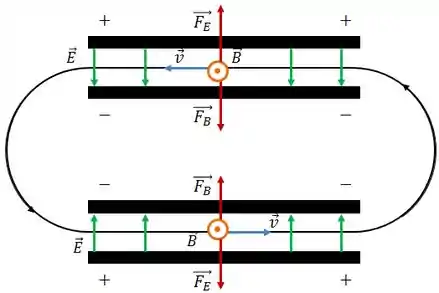
Na figura é mostrada a trajetória de um elétron em uma região na qual existe um campo magnético uniforme.
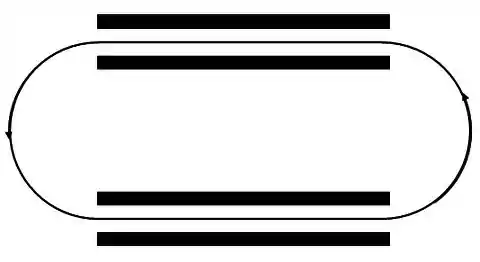
A trajetória é constituída por dois trechos retilíneos entre as duas placas uniformemente carregadas, e duas semicircunferências.
Dado o movimento entre do elétron segundo essa trajetória pode-se concluir que:
o campo magnético está dirigido para dentro da página e o potencial elétrico é maior na placa superior do conjunto das placas de cima;
o campo magnético está dirigido para fora da página e o potencial elétrico é maior na placa superior do conjunto das placas de cima;
os potenciais elétrico são maiores nas placas superiores dos dois conjuntos de placas carregadas;
o potencial elétrico é menor na placa superior do conjunto de placas superior e maior na placa superior do conjunto de placas inferior;
o campo magnético está dirigido para dentro da página e o potencial elétrico é menor na placa superior do conjunto das placas de cima.
Passo 1
Beleza, temos basicamente que analisar o sentido do campo magnético e o potencial elétrico das placas.
Vamos começar pelo campo magnético, beleza? Para isso, vamos olhar para o sentido das semicircunferências.
A força magnética sobre o elétron desempenha o trabalho de força centrípeta, mantendo o elétron na trajetória circular, e apontando sempre para o centro da trajetória, como mostrado abaixo:

Está representado acima também os vetores velocidade do elétron nos pontos escolhidos.
Passo 2
A força magnética sobre uma partícula pontual é dada por:
Como estamos trabalhando com um elétron (carga negativa), o sentido da força magnética será o sentido oposto ao do produto vetorial . Assim:

Podemos determinar o sentido do campo magnético utilizando a regra da mão direita, onde o dedo indicador representa o vetor , o polegar representa o produto vetorial e o dedo médio irá indicar o sentido do campo magnético.
Dessa forma, o campo magnético aponta para fora do plano da página.
Passo 3
Legal, agora vamos trabalhar com a questão do potencial das placas, beleza?
Bom, com o campo magnético para fora do plano da página, na região entre as placas a força magnética terá essa cara:
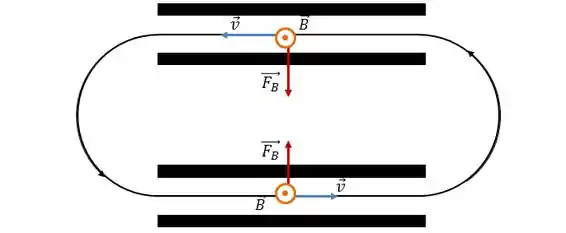
Como a trajetória que o elétron percorre entre as placas é retilínea, deve agir sobre ele uma força elétrica que anule a força magnética nessa região.
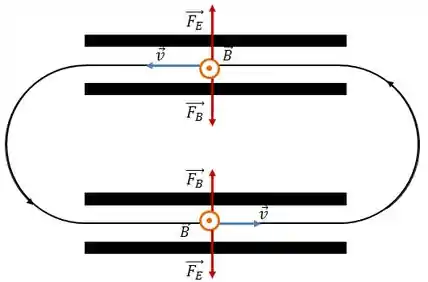
A força magnética sobre o elétron é dada por:
Onde é o vetor campo elétrico na região entre as placas. Novamente, como estamos trabalhando com um elétron, o campo elétrico deve ter o sentido contrário da força elétrica.
Assim, na região entre as placas teremos o seguinte:
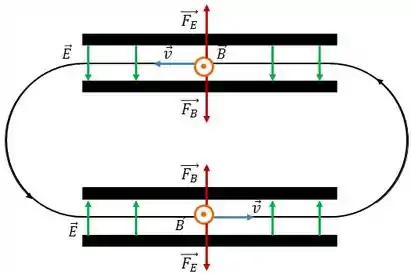
As linhas de campo magnético apontam da placa com maior potencial (indicada com sinal positivo) para a placa com menor potencial (indicada com sinal negativo), dessa forma, finalmente:
Passo 4
Analisando as alternativas, a resposta certa é a letra .
Resposta
o campo magnético está dirigido para fora da página e o potencial elétrico é maior na placa superior do conjunto das placas de cima;