UFF – Física 2 – Provas Antigas – P3 – 2022.1 – Questão 8
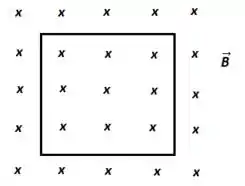
Na Figura, uma espira quadrada, com lado igual a , está imersa perpendicularmente em um campo magnético variável , onde é positivo para um campo apontando para dentro da página. Podemos afirmar que nos tempos e , os sentidos das correntes na espira tem as respectivas orientações:
a) A corrente é nula nos dois casos;
b) Nos dois casos o sentido é horário;
c) Nos dois casos o sentido é anti-horário;
d) Anti-horário e horário;
e) Horário e anti-horário.
Passo 1
Eaee!!! Belezinha? Olha.. nessa questão temos uma espira mergulhada perpendicularmente em um campo magnético que varia com o tempo pela seguinte fórmula:
Pois bem... para descobrir os sentidos da corrente em e , temos que analisar direitinho a fórmula.
Obs: Não se confunda ein! é a unidade de medida da densidade de campo magnético (militesla) 😉
Passo 2
Assim, avaliando a fórmula para o campo magnético, vemos que:
Para :
O campo está diminuindo sua intensidade (quanto mais próximo chega perto de , menor fica o campo.. experimenta substituir haha) e está orientado para dentro da página.
Dessa forma, no instante , de acordo com a Lei de Lenz, uma corrente induzida deve surgir no fio de modo a gerar um campo que se ponha a essa diminuição de intensidade.
Consequentemente, a corrente gera campo também entrando na página.
Logo, pela regra da mão direita, deve estar no sentido horário.
Passo 3
Ainda, avaliando a fórmula para o campo magnético, vemos que:
Para :
Nesse caso, o campo aumentará sua intensidade, ainda orientado no sentido para dentro da página.
Portanto, no instante de forma análoga, a corrente deverá estar no sentido anti-horário, visando gerar um campo que se oponha à variação de .
Dessa orma a alternativa correta é a letra e)!!!!
Entendeu direitinho? Responde aee ;)
Resposta
e) Horário e anti-horário.