Uma partícula tem seu movimento no plano descrito pela parametrização Então podemos afirmar que:
(a) a partícula passa pela reta
(b) nenhuma das outras alternativas.
(c) a partícula passa pela reta
(d) a partícula passa pela reta
(e) a partícula passa pela reta
Passo 1
A função é decrescente então
E como a exponencial é sempre positiva:
E também temos pras funções trigonométricas
Logo:
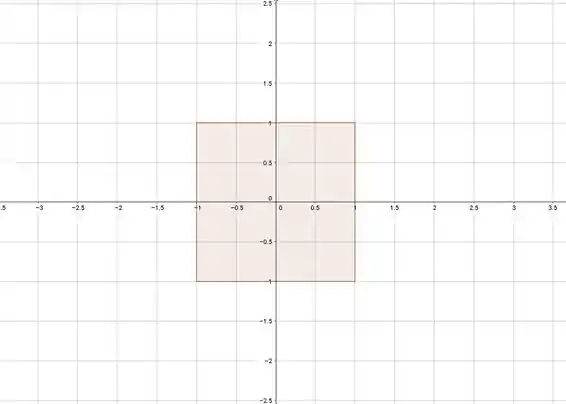
A partícula segue a parametrização ), então ela vai estar restrita a uma determinada área do plano, com
e
Que nada mais é que esse quadrado aqui
Passo 2
Show! Então vamos ver se alguma das retas que ele deu cruzam nosso quadrado! São as retas
São retas bem parecidas, na forma
Repare que por causa desse , nunca vamos ter ao mesmo tempo . Então as retas não cruzam o quadrado!
Vou acrescentá-las na nossa figura pra te convencer (na hora da prova você pode fazer uma também no canto da folha que é a boa):
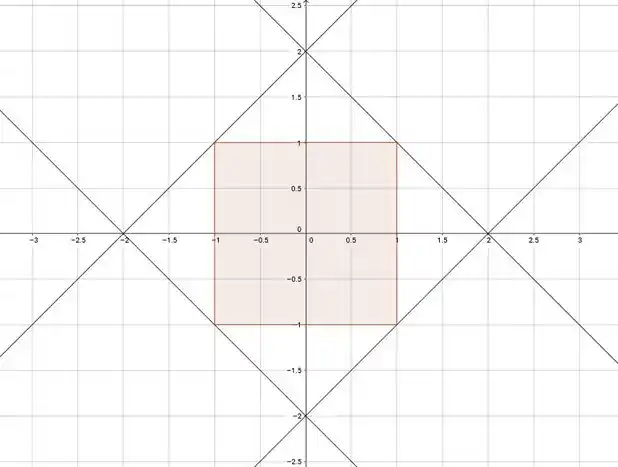
As retas passam raspando mas não cruzam o quadrado! E se fosse considerar essa raspada teríamos 4 alternativas certas né, então a resposta é a letra (b)!
Resposta
Alternativa (b)