Uma bateria comercial de é utilizada no circuito esquematizado abaixo, no qual o amperímetro e o voltímetro são considerados ideais.
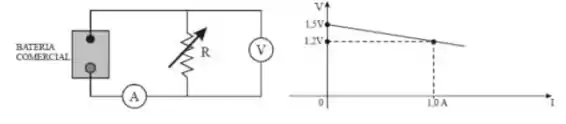
Varia-se a resistência , e as correspondentes indicações do amperímetro e do voltímetro são usadas para construir o seguinte gráfico de voltagem versus intensidade de corrente . Usando as informações do gráfico, calcule: o valor da resistência interna da bateria.
Passo 1
Para começarmos a solução desse problema, é importante fazermos uma revisão rápida do que são voltímetros e amperímetros ideais.
Um amperímetro é utilizado para medir corrente elétrica: a corrente passar dentro dele e ele mede esse valor. Quando é ideal, o amperímetro tem sua resistência interna igual a zero e, por isso, não vai ter ddp entre seus terminais, apesar de a corrente passar por dentro dele.
Já um voltímetro é utilizado para medir ddp’s. A gente coloca o voltímetro em paralelo com a parte do circuito da qual queremos saber a ddp. O voltímetro ideal vai ser aquele que tem uma resistência interna tão grande (“infinita”) que por dentro dele não passa nenhuma corrente e, por isso, a ddp que ele vai medir vai ser somente relacionada aquela parte do circuito que estamos analisando.
Bom, depois disso, vamos ver como encontrar a resistência interna da bateria. Bora??
Passo 2
Primeiro, vamos precisar do gráfico que o problema deu. À medida que varia, a voltagem e a corrente entre seus terminais variam. Por isso, dá uma olhada lá na figura: quando , temos , ou seja, não passa corrente no circuito e a ddp medida é igual à ddp da própria bateria.
Agora, quando , a ddp entre os terminais do resistor é igual a . Com essa corrente, vamos utilizar a lei das malhas para o circuito, considerando que a resistência interna da bateria é e é o valor dela que queremos achar.
Portanto, para esses valores, teremos:
Resposta
Letra a.