Na figura abaixo as fontes ideais têm forças eletromotrizes e e os resistores têm resistências Determine:
- a corrente do circuito;
- a potência dissipada no resistor ;
- a potência dissipada no resistor ;
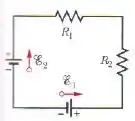
Passo 1
Então, pessoal! Temos uma malha simples. Vamos devagar, aprendendo a cada passo.
Ele nos forneceu o valor das duas fontes e dos resistores e está pedindo pra a gente calcular primeiramente a corrente nesse circuito.
Como fazer? Vamos lá!
Passo 2
a)
Só relembrando as regrinhas:
Resistência
- Quando atravessamos uma resistência no sentido da corrente, a diferença de potencial é ;
- Quando atravessamos uma resistência no sentido oposto ao da corrente, a diferença de potencial é ;
Fonte
- Quando atravessamos uma fonte do terminal negativo (barra menor) para o positivo (barra maior), a diferença de potencial é ;
- Quando atravessamos uma fonte do terminal positivo para o negativo, a diferença de potencial é ;
Passo 3
Pela Lei das Malhas de Kirchhoff, a soma das ddp’s nesse circuito tem que ser zero.
Mas, nesse caso nós temos duas forças eletromotrizes, como vamos saber o sentido da corrente? Relaxa, nós podemos supor um sentido para a corrente. Supondo que esse seja o sentido horário, logo, teremos que:
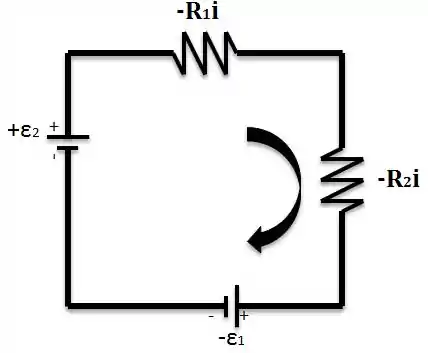
Isolando o teremos:
Como achamos um valor negativo para a corrente, podemos afirmar que supomos o sentido errado! Analisando o circuito podemos visualizar isso, afinal o sentido da corrente vai ser definido pela fonte de maior potencial no caso , ou seja o sentido da fonte é anti-horário.
Passo 4
b)
Aqui é só relembrar a formulinha de potência. Como aqui temos resistência e também a corrente é só usar:
Passo 5
c)
Mesma coisa da letra b, só trocando os valores.
E é isso aê!