- Na figura abaixo qual deve ser o valor de para que a corrente no circuito seja ?
Sabe-se que , , .
- Qual é a potência dissipada em
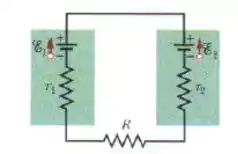
Passo 1
a)
Ele nos dá as informações dos dois geradores e das suas resistências internas e ainda nos dá a corrente . Só o que sobra pra a gente é que? O resistor . Vai sair bem rápido usando Lei das Malhas. Saca só!
Passo 2
Vamos supor esse sentido indicado para a corrente e uma malha sentido horário.
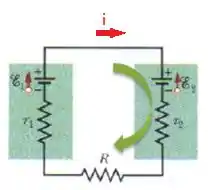
Usando o mesmo sentido (horário) para a Lei das Malhas do nosso amigo Kirchhoff, teremos:
Isolando o , teremos:
Como encontramos um valor negativo para , erramos no sentido da corrente!
Mas, calma! Fazendo de novo, agora para uma corrente no sentido anti-horário. Usando o sentido anti-horário também para a Lei das Malhas, obtemos:
Agora sim!
Passo 3
b)
Lembra como calcula a potência somente?
Primeiro temos que ver o que a gente tem. Nesse caso, temos a resistência que a gente acabou de achar e também a corrente.
Calculando a potência com esses dados é só usar: