Na figura abaixo mostre que a potência dissipada em é máxima para . Mostre que essa potência máxima é .
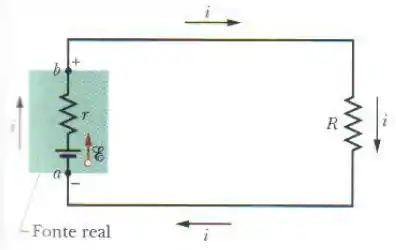
Passo 1
Opa! Primeiro de tudo, é bom ter uma noção quais as variáveis nós precisamos lidar para poder resolver esse problema. Ele fala em potência e a gente já vê na figura as grandezas e .
Pra calcular a potência no resistor com esses dados é só usar
Passo 2
Mas a gente não sabe quem é , então vamos busca-la!
Pela Lei das Malhas, adotando o sentido da corrente, teremos:
Show?
Show!
Passo 3
Agora é só tacar lá na fórmulinha da potência.
Passo 4
Mas pera, agora vamos entrar no mais delicado da questão.
Vemos que pra uma dada fonte com ddp e , para cada valor pra teremos um valor pra . Assim, podemos dizer que é uma função de e pra otimizar essa função temos que derivar e igualar a zero. Lembra lá do cálculo? Espero que sim. :}
Derivando, pela regra do quociente, vamos ter:
Fazendo o MMC disso aí, vamos ter:
Passo 5
Agora é só substituir o valor de lá na potência. Daí, teremos:
Como queríamos demonstrar!!
Resposta
Ei, a resposta está no passo a passo :)