Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Circuito de uma Malha

Ver Teoria
Exercício 241234567891011121314151617181920212223

Enunciado

A figura abaixo mostra quatro possíveis arranjos de três capacitores idênticos. Os valores das capacitâncias equivalentes de cada arranjo são C 1 , C 2 , C 3 e C 4 .

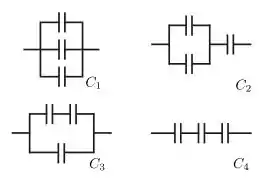
Nessa situação, é correto afirmar que:

  1. C 1 > C 3 > C 2 > C 4
  2. C 1 > C 2 > C 3 > C 4
  3. C 1 > C 3 = C 2 > C 4
  4. C 4 > C 2 > C 3 > C 1
  5. C 4 > C 3 > C 2 > C 1
  6. C 4 > C 3 = C 2 > C 1
  7. C 2 > C 3 > C 4 > C 1
  8. C 3 > C 2 > C 4 > C 1

Passo 1

Bem, de acordo com a nossa teoria, capacitores em paralelo, como é o caso do C 1 ...

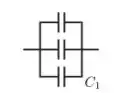
Para encontrar a capacitância total ( C 1 ) você pode simplesmente somar todas as três capacitâncias C ...

C 1 = 3 C

Todavia, contudo, não obstante... Para capacitores em série, como é o caso do C 4 ...

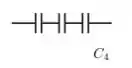
Você pode encontrar a capacitância total C 4 fazendo...

1 C 4 = 1 C + 1 C + 1 C = 3 C

Os outros dois vai ser as duas coisas juntas! Vamos ver isso com mais calma?

Passo 2

Já encontramos a capacitância C 1 em termos da capacitância C de um capacitor...

C 1 = 3 C

E o C 4 também...

1 C 4 = 3 C     →

C 4 = C 3

Agora para o C 2 ...

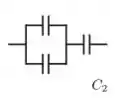
Veja que primeiro temos um paralelo entre dois capacitores C , logo isso vai gerar uma capacitância parcial de C p a r = 2 C ...

E aí para encontrar o C 2 , a gente usa o conceito de capacitores em série...

1 C 2 = 1 C p a r + 1 C   →

1 C 2 = C + C p a r C p a r C   →

C 2 = C p a r C C + C p a r

Como C p a r = 2 C ...

C 2 = 2 C 2 C + 2 C = 2 C 2 3 C   →

C 2 = 2 3 C

Passo 3

Agora vamos fazer algo parecido para encontrar o C 3 ...

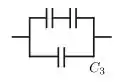
Mas primeiro a gente vai juntar os dois de cima que estão em série em uma única capacitância parcial C p a r ...

E depois a gente usa o paralelismo de C p a r com o C de baixo para determinar C 3 ...

C 3 = C p a r + C

Só que o C p a r é então proveniente da série entre os dos capacitores C ...

1 C p a r = 1 C + 1 C   →

1 C p a r = 2 C     →           C p a r = C 2

Então...

C 3 = C p a r + C   →

C 3 = C 2 + C = 3 2 C

Passo 4

Agora é só comparar mesmo...

C 1 = 3 C

C 2 = 2 3 C

C 3 = 3 2 C

C 4 = C 3

Então...

C 1 > C 3 > C 2 > C 4

Resposta

Letra A

Exercícios de Livros Relacionados

Uma lâmpada de 120V e 25.0W está conectada em série com uma Lâmpada de 120V é aplicada à combinação. Considere que as lâmpadas tenham resistências constantes. (a) Qual lâmpada deveria ser mais brilhan
A lei das junções de Kirchhoff é considerada como uma consequência de (a) conservação de carga, (b) conservação de energia, (c) leis de Newton, (d) lei de Coulomb, (e) quantização da carga elétrica.
Um laser de diodo usado para fazer uma ponteira laser é um elemento de circuito altamente não linear. Seu comportamento está descrito a seguir. Para qualquer queda de tensão sobre ele que seja menor q
Na Fig. 27-84, R 1=R 2=2,0Ω ,R 3=4,0Ω ,R 4=3,0Ω ,R 5=1,0Ω ,R 6=R 7=R 8=8,0Ω e as forças eletromotrizes das fontes são ε 1=16V e ε 2 =8,0V . Determine: (a) o valor absoluto e (b) o sentido (para cima o
Na Fig. 27-81, as forças eletromotrizes das fontes ideais são ε 1 =20,0V ,ε 2 =10,0V ,ε 3 =5,00V e ε 4=5,00V , e todas as resistências são de 2,00Ω . Determine (a) o valor absoluto e (b) o sentido (pa