Exercícios Resolvidos de Circuito RLC com fonte

Enunciado

Após estar aberta por um dia, a chave do circuito abaixo é fechada em Determine a equação diferencial que descreve .

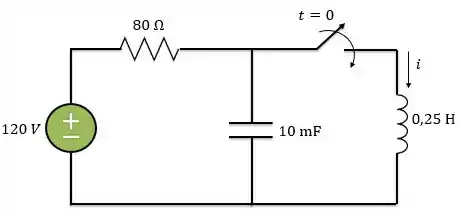
Passo 1

Nesse exercício não precisamos encontrar como se comporta a corrente para . Precisamos encontrar a EDO de segunda ordem que descreve essa corrente.

Nós vimos que é possível encontrar sem precisarmos encontrar a EDO antes. Mas na realidade, como vimos na teoria, tudo parte de uma EDO de segunda ordem não homogênea. A partir dela chegamos nos casos de amortecimento e nas soluções gerais.

Passo 2

Para começar, vamos aplicar a LCK ao nó do circuito abaixo.

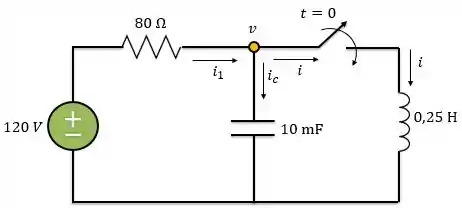
Pela lei de Ohm,

Substituindo,

Arrumando a equação, temos

Passo 3

Como o indutor está em paralelo com o capacitor, eles possuem a mesma tensão . Portanto, no indutor

Como queremos encontrar uma EDO para a corrente, vamos substituir a equação em .

Arrumando a EDO,

Para terminar, dividindo todos os termos por ,

Resposta

Exercícios de Livros Relacionados

Para o circuito da Figura 8.65, determine:(a) v 0 +ei ( 0 + ) (b) d v ( 0 + ) / d ted i ( 0 + ) / d t (c) v ∞ei ( ∞ )

Calcule v para t0 , se o circuito está em regime permanente em t = 0 - ,

Referindo-se ao circuito da Figura 8.66, determine:(a) i ( 0 + ) e v ( 0 + ) (b) d i ( 0 + ) / d t e d v ( 0 + ) / d t (c) i ( ∞ ) e v ( ∞ )

Usando a Figura 8.9 3 , elabore um problema para ajudar outros estudantes a entenderem melhor a resposta a um degrau de um circuito R L C em paralelo.

Obtenha v(t) e i(t) para t0 no circuito da Figura 8.84.