Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Circuito RLC com fonte

Ver Teoria
Exercício 81234567910

Enunciado

No circuito abaixo, determine v t e i ( t ) para t > 0 . Suponha v 0 = 0   V e i 0 = 1   A .

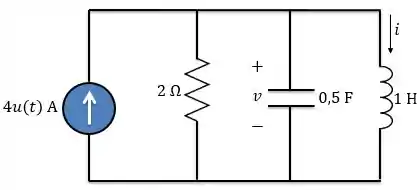
Passo 1

Esse é um circuito R L C paralelo clássico. O enunciado já nos deu de bandeja duas condições iniciais. Primeiro vamos determinar a corrente i ( t ) . Então, precisamos encontrar a condição inicial da derivada da corrente.

Passo 2

Como o circuito é paralelo, a tensão é a mesma para todos os elementos. Logo, no indutor

v = L d i d t

Em t = 0 + , como a tensão no capacitor não pode variar instantaneamente,

v 0 + = v 0 - = 0

Portanto,

v 0 + = 1 d i ( 0 + ) d t = 0

d i 0 + d t = 0

Passo 3

Agora que encontramos as condições iniciais, vamos encontrar os parâmetros α e ω 0 , para sabermos qual o tipo de amortecimento do circuito.

Sabemos que no circuito R L C paralelo

α = 1 2 R C = 1 2 2 0,5 = 0,5

ω 0 = 1 L C = 1 0,5 = 2

Como α < ω 0 , temos o caso de subamortecimento. Onde sua solução geral é

i t = I G + e - α t A c o s   ω d t + B s i n   ω d t

Onde, I G é a corrente da fonte e ω d = ω 0 2 - α 2 .

I G = 4   A

ω d = 2 - 0,25 = 1,323

Então, para esse circuito a corrente tem a seguinte expressão:

i t = 4 + e - 0,5 t A   c o s   1,323 t + B s i n   1,323 t

Passo 4

Agora, precisamos determinar o valor de cada constante. Faremos isso, usando nossas condições iniciais.

i t = 4 + e - 0,5 t A c o s   1,323 0 + B s i n   1,323 ( 0 ) = 1

4 + A = 1

A = - 3

Derivando i t , temos

d i d t = - 0,5 e - 0,5 t A c o s   1,323 t + B s i n   1,323 t + e - 0,5 t 1,323 ( - A sin ⁡ 1,323 t + B cos ⁡ 1,323 t )  

Logo,

d i 0 + d t - 0,5 A + 1,323 B = 0

B = 0,5 - 3 1,323 = - 1,134

Portanto, substituindo os valores das constantes, a solução completa final é

i t = 4 + e - 0,5 t - 3 c o s   1,323 t - 1,134 s i n   1,323 t     A

Passo 5

Agora que já encontramos a corrente que passa pelo indutor, vamos encontrar a tensão v ( t ) .

A gente já sabe que v ( t ) é a mesma para todos os elementos do circuito.

Como no indutor,

v = L d i d t

Basta derivarmos a corrente i ( t ) e multiplicá-la pelo valor do indutor. Nós acabamos de derivar a corrente no passo anterior e vimos que:

d i d t = - 0,5 e - 0,5 t A c o s   1,323 t + B s i n   1,323 t + e - 0,5 t 1,323 ( - A sin ⁡ 1,323 t + B cos ⁡ 1,323 t )

Substituindo o valor de cada constante:

d i d t = - 0,5 e - 0,5 t - 3 c o s   1,323 t - 1,134 s i n   1,323 t + e - 0,5 t 1,323 ( 3 sin ⁡ 1,323 t - 1,134 cos ⁡ 1,323 t )

d i d t = 1,5 e - 0,5 t c o s   1,323 t + 0,567 e - 0,5 t s i n   1,323 t + ( 3,969 e - 0,5 t sin ⁡ 1,323 t - 1,5 e - 0,5 t cos ⁡ 1,323 t )

d i ( t ) d t = 4,536 e - 0,5 t sin ⁡ 1,323 t

Como, L = 1   H

v t = d i ( t ) d t = 4,536 e - 0,5 t sin ⁡ 1,323 t     V

Resposta

i t = 4 + e - 0,5 t - 3 c o s   1,323 t - 1,134 s i n   1,323 t     A

v t = 4,536 e - 0,5 t sin ⁡ 1,323 t     V

Exercícios de Livros Relacionados

Para o circuito da Figura 8.65, determine:(a) v 0 +ei ( 0 + ) (b) d v ( 0 + ) / d ted i ( 0 + ) / d t (c) v ∞ei ( ∞ )
Calcule v para t0 , se o circuito está em regime permanente em t = 0 - ,
Referindo-se ao circuito da Figura 8.66, determine:(a) i ( 0 + ) e v ( 0 + ) (b) d i ( 0 + ) / d t e d v ( 0 + ) / d t (c) i ( ∞ ) e v ( ∞ )
Usando a Figura 8.9 3 , elabore um problema para ajudar outros estudantes a entenderem melhor a resposta a um degrau de um circuito R L C em paralelo.
Obtenha v(t) e i(t) para t0 no circuito da Figura 8.84.