Determine as correntes de estado estacionário e para o circuito na figura:
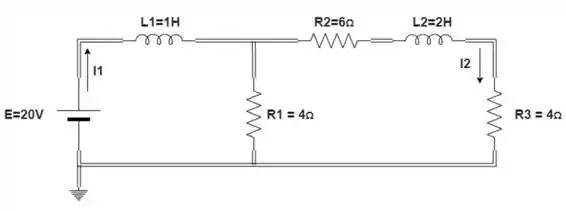
Passo 1
Substituir o indutor por um curto-circuito, por onde passa a corrente e substituir o indutor por um curto circuito por onde passa a corrente .
Passo 2
Assim temos um circuito simples, onde está em série com o resistor e estão em paralelo com o resistor .
Vamos calcular a resistência equivalente do circuito para calcular a corrente total que sai da fonte .
Passo 3
A corrente total é dada por:
Passo 4
A corrente total é calculada através do divisor de corrente entre os ramos do circuito: