Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Circuito RLC com fonte

Ver Teoria
Exercício 61234578910

Enunciado

Determine v t para t > 0 no circuito abaixo.

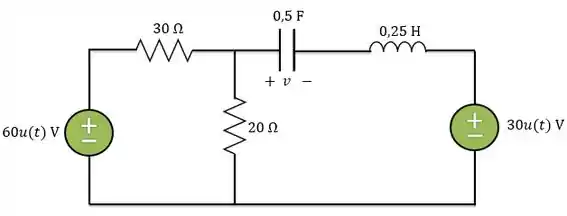
Passo 1

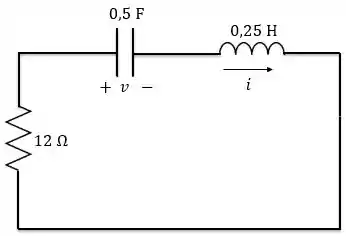
Como a gente pode ver, esse circuito não é um circuito R L C série nem paralelo, é um circuito de segunda ordem qualquer. Antes de mais nada, vamos determinar nossas condições iniciais e finais para a tensão v .

Para t = 0 - , as fontes de tensão valem zero, já que para t < 0 ,   u t = 0 . Ou seja, podemos considerar que não há energia armazenada no circuito.

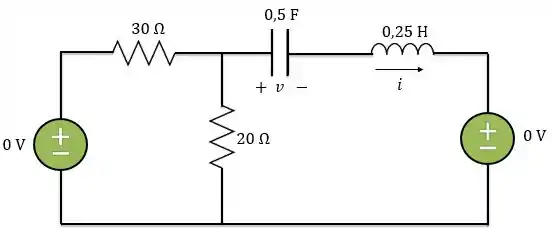
Logo,

v 0 - = 0

i 0 - = 0

Passo 2

Como a tensão no capacitor não pode variar instantaneamente, assim como a corrente no indutor, temos que

v 0 + = v 0 - = 0

i 0 + = i 0 - = 0

Ainda precisamos determinar d v ( 0 + ) / d t . Sabemos que no capacitor

i c = C d v d t

Como o capacitor e o indutor estão em série, a corrente neles é a mesma. Logo,

i c 0 + = i 0 + = 0

Portanto,

d v 0 + d t = i 0 + 0,5

d v 0 + d t = 0 0,5 = 0

Passo 3

Agora, precisamos encontrar o valor final da tensão no capacitor. Isso ocorre quando t → ∞ e podemos considerar que o circuito atingiu o regime permanente, no qual o indutor pode ser considerado um curto-circuito e o capacitor um circuito-aberto.

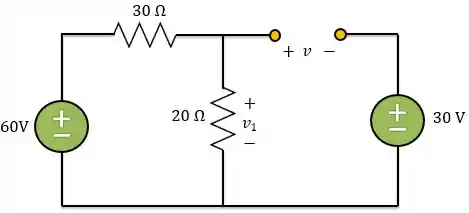
Aplicando LTK, na malha da direita, temos

- v 1 ∞ + v ∞ + 30 = 0

v ∞ = v 1 ∞ - 30

Aplicando divisor de tensão, encontramos a tensão v 1 :

v 1 ∞ = 20 20 + 30 × 60

v 1 ( ∞ ) = 24   V

Logo, o valor final da tensão no capacitor é:

v ∞ = 24 - 30 = - 6   V

Esse valor final é a resposta forçada do circuito,

v p t = v ∞ = - 6   V

Passo 4

Pronto, encontramos todas os nossos valores iniciais e a resposta forçada. Agora, vamos encontrar a resposta natural v h ( t ) para t > 0 . Para isso, precisamos desligar todas as fontes independentes do circuito.

Lembrando que desligar uma fonte de tensão é o mesmo que considerá-la um curto-circuito. Logo, teremos o circuito abaixo:

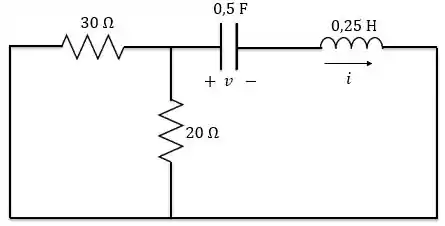
Fazendo a associação dos resistores em paralelo, temos

R e q = 20   ×   30 20 + 30 = 12   Ω

Olha que maravilha! Chegamos ao circuito R L C série sem fontes e nele sabemos que:

α = R 2 L = 12 0,5 = 24

ω 0 = 1 L C = 1 ( 0,25 ) ( 0,5 ) = 2,828

Como α > ω 0 , temos o caso superamortecido. Esse caso tem a seguinte solução geral:

v h t = A e r 1 t + B e r 2 t

Onde as raízes são,

r 1,2 = - α ± α 2 - ω 0 2

Substituindo os valores de α e ω 0 , temos

r 1,2 = - 24 ± 24 2 - 2,838 2

Logo,

r 1 = - 0,168

r 2 = - 47,83

Portanto, nossa resposta natural é

v h t = A e - 0,168 t + B e - 47,83 t

Passo 5

A solução completa é a soma da resposta natural com a resposta forçada.

v t = v h t + v p t

v t = A e - 0,168 t + B e - 47,83 t - 6

Agora, precisamos determinar o valor de cada constante. Faremos isso, usando nossas condições iniciais.

v 0 + = A e - 0,168 0 + B e - 47,83 0 - 6 = 0

A + B = 6

Derivando v t , temos

d v d t = - 0,168 A e - 0,168 t - 47,83 B e - 47,83 t

Logo,

d v 0 + d t = - 0,168 A e - 0,168 ( 0 ) - 47,83 B e - 47,83 ( 0 ) = 0

- 0,168 A - 47,83 B = 0

Resolvendo o sistema abaixo,

A + B = 6 - 0,168 A - 47,83 B = 0

Isolando A na primeira equação e substituindo na segunda, temos

- 0,168 6 - B - 47,83 B = 0

- 1,008 + 0,168 B - 47,83 B = 0

- 47,66 = 1,008

B = - 0,021

Logo,

A = 6 - ( - 0,021 ) = 6,021

Portanto, a solução completa final é:

v t = 6,021 e - 0,168 t - 0,021 e - 47,83 t - 6       V

Resposta

v t = 6,021 e - 0,168 t - 0,021 e - 47,83 t - 6       V

Exercícios de Livros Relacionados

Para o circuito da Figura 8.65, determine:(a) v 0 +ei ( 0 + ) (b) d v ( 0 + ) / d ted i ( 0 + ) / d t (c) v ∞ei ( ∞ )
Calcule v para t0 , se o circuito está em regime permanente em t = 0 - ,
Referindo-se ao circuito da Figura 8.66, determine:(a) i ( 0 + ) e v ( 0 + ) (b) d i ( 0 + ) / d t e d v ( 0 + ) / d t (c) i ( ∞ ) e v ( ∞ )
Usando a Figura 8.9 3 , elabore um problema para ajudar outros estudantes a entenderem melhor a resposta a um degrau de um circuito R L C em paralelo.
Obtenha v(t) e i(t) para t0 no circuito da Figura 8.84.