Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Circuito RLC com fonte

Ver Teoria
Exercício 31245678910

Enunciado

Determine v t para t > 0 no circuito abaixo.

Passo 1

Antes de mais nada, vamos determinar nossas condições iniciais e finais para a tensão v .

Para t = 0 - , a chave está fechada e o circuito já atingiu o regime permanente. Então, podemos considerar o indutor um curto-circuito e o capacitor um circuito aberto.

Além disso, a fonte de corrente da esquerda vale zero, já que para t < 0 ,   u t = 0 . Ou seja, podemos considerá-la desligada.

Passo 2

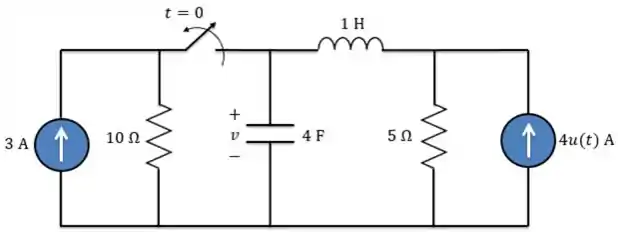
Então, para t = 0 - , analisamos o circuito abaixo.

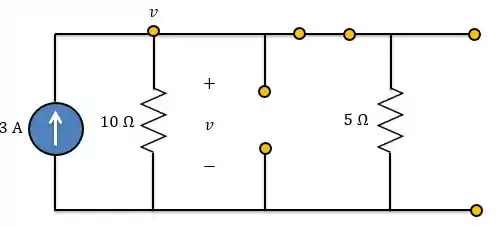
Redesenhando

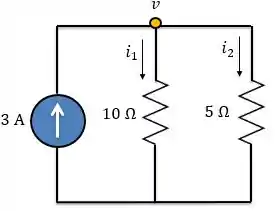
Aplicando LCK ao nó,

3 = i 1 + i 2

3 = v ( 0 - ) 10 + v ( 0 - ) 5

3 v 0 - = 30

v 0 - = 10   V

Se repararmos, i 2 é a corrente que passa pelo indutor e seu valor será

i 2 0 - = 10 5 = 2   A

Passo 3

Precisamos encontrar a condição inicial para a derivada da tensão. Em t = 0 + , a chave é aberta e temos o seguinte circuito.

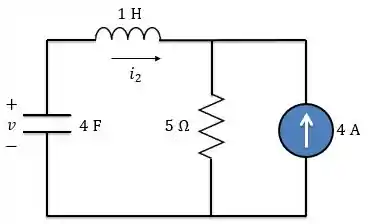
Agora vamos fazer uma coisa que vai facilitar muito: usar transformação de fontes. A fonte de corrente que está em paralelo com o resistor vai se transformar numa fonte de tensão em série com o resistor. Lembra disso?

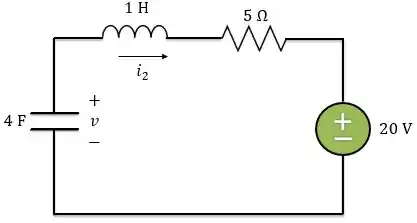
O circuito acima nós conhecemos bem! É o circuito R L C série.

Lembrando que a fonte de tensão tem valor de 20   V , porque quando realizamos a transformação de fontes temos que respeitar a lei de Ohm

V = 5 × 4 = 20   V

Passo 4

Como a tensão no capacitor não pode variar instantaneamente, assim como a corrente no indutor, temos que

v 0 + = v 0 - = 10   V

i 2 0 + = i 2 0 - = 2   A

Ainda precisamos determinar d v ( 0 + ) / d t . Sabemos que no capacitor

i c = C d v d t

Como o circuito é série, a corrente em todos os elementos é a mesma. Logo,

i c 0 + = i 2 0 + = 2   A

Temos que tomar cuidado agora. Veja que a corrente i 2 está no sentido contrário a convenção de sinais em elementos passivos no capacitor. Logo,

i 2 = - C d v d t

Portanto,

d v 0 + d t = - i 2 0 + 4  

d v 0 + d t = - 2 4 = - 0,5   V / s

Passo 5

Agora, precisamos encontrar o valor final. Isso ocorre quando t → ∞ e podemos considerar um novo regime permanente, no qual mais uma vez o indutor pode ser considerado um curto-circuito e o capacitor um circuito-aberto.

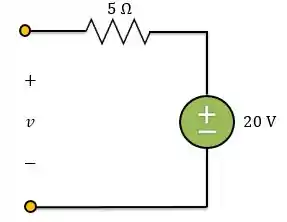
Como o circuito está aberto, não há circulação de corrente e, consequentemente, queda de tensão no resistor. Portanto, a tensão v será a própria tensão da fonte.

v ∞ = 20   V

Passo 6

Pronto, encontramos todas os nossos valores iniciais e finais. Agora, vamos encontrar a expressão para v ( t ) para t > 0 .

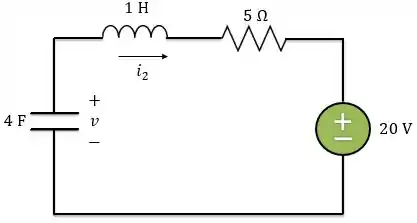
Como o circuito é R L C série sabemos que

α = R 2 L = 5 2 = 2,5

ω 0 = 1 L C = 1 4 = 0,5

Como α > ω 0 , temos o caso superamortecido. Esse caso tem a seguinte solução geral.

v t = v ( ∞ ) + A e r 1 t + B e r 2 t

Onde as raízes são,

r 1,2 = - α ± α 2 - ω 0 2

Substituindo os valores de α e ω 0 , temos

r 1,2 = - 2,5 ± 2,5 2 - 0 , 5 2

Logo,

r 1 = - 0,0505

r 2 = - 4,949

Portanto, nossa solução completa é

v t = 20 + A e - 0,0505 t + B e - 4,949 t

Passo 7

Agora, precisamos determinar o valor de cada constante. Faremos isso, usando nossas condições iniciais.

v 0 + = 20 + A e - 0,0505 ( 0 ) + B e - 4,949 ( 0 ) = 10

A + B = - 10

Derivando v t , temos

d v d t = - 0,0505 A e - 0,0505 t - 4,949 B e - 4,949 t

Logo,

d v 0 + d t = - 0,0505 A e - 0,0505 ( 0 ) - 4,949 B e - 4,949 ( 0 ) = - 0,5

- 0,0505 A - 4,949 B = - 0,5

Resolvendo o sistema abaixo,

A + B = - 10 - 0,0505 A - 4,949 B = - 0,5

Isolando A na primeira equação e substituindo na segunda, temos

- 0,0505 - 10 - B - 4,949 B = - 0,5

0,505 + 0,0505 B - 4,949 B = - 0,5

- 4,8985 B = - 1,005

B = 0,205

Logo,

A = - 10 - 0,205 = - 10,205

Portanto, a solução completa final é

v t = 20 - 10,205 e - 0,0505 t + 0,205 e - 4,949 t     V

Resposta

v t = 20 - 10,205 e - 0,0505 t + 0,205 e - 4,949 t     V

Exercícios de Livros Relacionados

Para o circuito da Figura 8.65, determine:(a) v 0 +ei ( 0 + ) (b) d v ( 0 + ) / d ted i ( 0 + ) / d t (c) v ∞ei ( ∞ )
Calcule v para t0 , se o circuito está em regime permanente em t = 0 - ,
Referindo-se ao circuito da Figura 8.66, determine:(a) i ( 0 + ) e v ( 0 + ) (b) d i ( 0 + ) / d t e d v ( 0 + ) / d t (c) i ( ∞ ) e v ( ∞ )
Usando a Figura 8.9 3 , elabore um problema para ajudar outros estudantes a entenderem melhor a resposta a um degrau de um circuito R L C em paralelo.
Obtenha v(t) e i(t) para t0 no circuito da Figura 8.84.