Calcule a constante de tempo do circuito abaixo
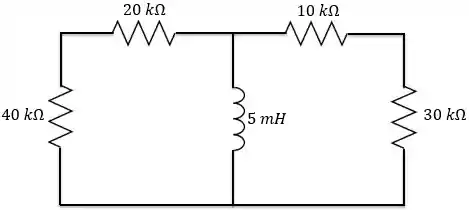
Passo 1
O circuito acima possui um indutor e vários resistores. Para encontrarmos o valor da constante de tempo, precisamos transformar esse circuito no circuito RL sem fonte que conhecemos.
Passo 2
Para isso, vamos calcular a resistência equivalente de Thévenin nos terminais do indutor.
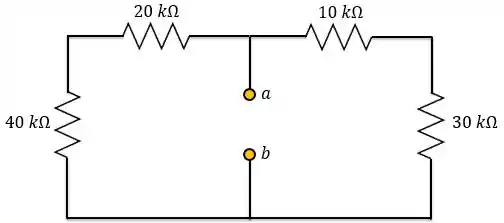
Fazendo a associação em série dos resistores:
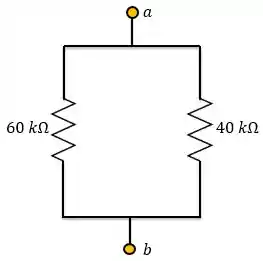
Passo 3
Como esses resistores estão associados em paralelo:
Passo 4
Pronto, agora que encontramos , chegamos ao nosso circuito RL sem fonte, com apenas um resistor e um indutor.
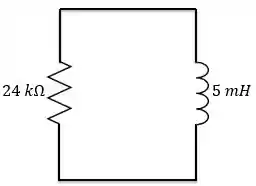
A gente conhece a constante de tempo para esse circuito.
Substituindo os valores:
Resposta
Exercícios de Livros Relacionados
A questão quer que o aluno mostre que o resistor tem uma certa equação, e em seguida comparar com o resultado da questão anterior.
Essa questão é interessante, uma vez que se pode escolher qual configuração pode ser usada
Calcule i para t0 , se i (0) = 4 A e i_g = 8 A
O pulso na figura 7.116a pode ser expressa em termos de funções de singularidade como: a2 u t + 2 u t - 1V b2 u t - 2 u t - 1V c2 u t - 4 u t - 1V d2 u t + 4 u t - 1V
A constante de tempo para um circuito R L com R = 2 Ω e L = 4 H é:(a) 0,5 s (b) 2 s (c) 4 s (d) 8 s (e) 15 s