Determine e para no circuito abaixo se
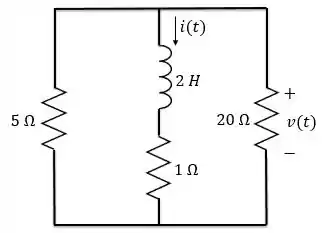
Passo 1
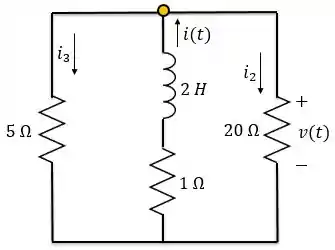
O circuito acima possui um indutor e vários resistores. Precisamos transformá-lo no circuito RL sem fonte com apenas um resistor e um indutor, para encontrarmos a corrente e a tensão .
Passo 2
Para isso, vamos calcular a resistência equivalente de Thévenin nos terminais do indutor.
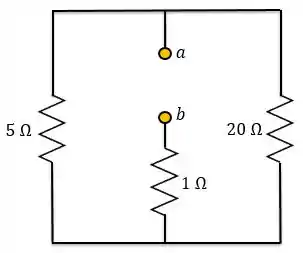
Vamos ajeitar o circuito para visualizar melhor e ajudar a gente.
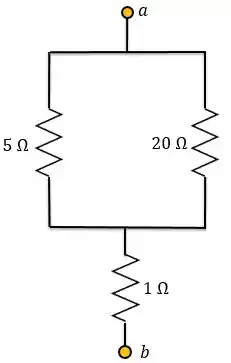
Passo 3
Logo, a gente vê que o resistor de está em série com a associação em paralelo dos resistores de e .
Passo 4
Pronto, agora que encontramos , chegamos ao nosso circuito RC sem fonte, com apenas um resistor e um indutor.
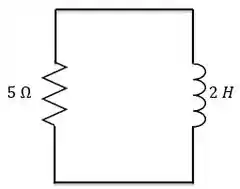
A gente conhece a constante de tempo para esse circuito.
Substituindo os valores:
Passo 5
A gente viu na teoria que a corrente nesse circuito tem a seguinte relação geral:
Onde
Logo,
Passo 6
Aplicando divisor de corrente, a gente encontra a corrente que passa pelo resistor de .
Esse sinal de menos apareceu na corrente , pois a gente inverteu o seu sentido, originalmente ela estava saindo do nó, mas para o cálculo do divisor de corrente consideramos ela entrando no nó.
Passo 7
Agora é só aplicar a boa e velha lei de Ohm para encontrarmos a tensão .