Considerando o circuito da figura:
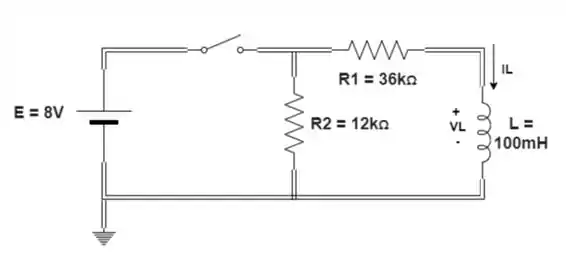
- Determine as expressões matemáticas para a corrente e para a tensão quando a chave é fechada.
- Repita o item (a) se a chave for aberta após a passagm de cinco constantes de tempo.
Passo 1
Primeiro devemos calcular o equivalente Thévenin entre o terminais do indutor, para isso devemos substituir a fonte de tensão por um curto circuito:
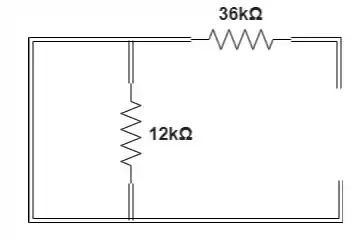
Enquanto a tensão é igual a tensão a fonte 8V.
Passo 2
Podemos calcular a constante de tempo para o momento de carregamento :
Passo 3
Após a chave ser fechada, a corrente que circula pelo indutor é dada pela fórmula:
Passo 4
A tensão sobre o indutor, segue a equação:
Passo 5
Após 5 constantes de tempo, o indutor irá descarregar a partir de um valor inicial igual a:
Passo 6
A nova constante de tempo para o circuito enquanto o indutor descarrega é:
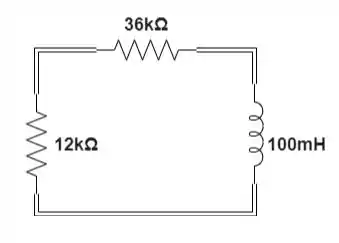
Passo 7
A tensão sobre o indutor descarregando segue a fórmula, onde já calculamos o valor inicial de :
Passo 8
A corrente que passa pelo indutor segue a fórmula:
Resposta
a)
V
b)
Exercícios de Livros Relacionados
A questão quer que o aluno mostre que o resistor tem uma certa equação, e em seguida comparar com o resultado da questão anterior.
Essa questão é interessante, uma vez que se pode escolher qual configuração pode ser usada
Calcule i para t0 , se i (0) = 4 A e i_g = 8 A
O pulso na figura 7.116a pode ser expressa em termos de funções de singularidade como: a2 u t + 2 u t - 1V b2 u t - 2 u t - 1V c2 u t - 4 u t - 1V d2 u t + 4 u t - 1V
A constante de tempo para um circuito R L com R = 2 Ω e L = 4 H é:(a) 0,5 s (b) 2 s (c) 4 s (d) 8 s (e) 15 s