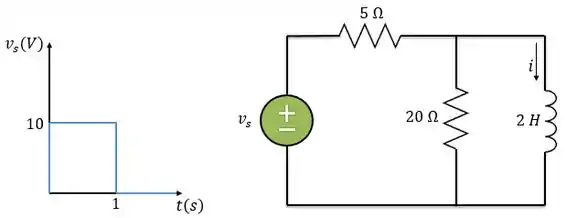
Se o pulso de entrada do gráfico abaixo for aplicado ao circuito, determine a resposta .

Agora, vamos analisar no intervalo de . Nesse intervalo a fonte de tensão vale . Vamos analisar o circuito abaixo para encontrarmos a corrente nesse intervalo.

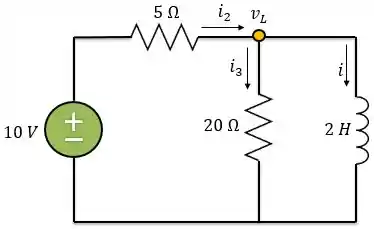
Primeiro, vamos aplicar a LCK ao nó:

Sabemos que a tensão no indutor tem a seguinte relação:

E como o indutor está em paralelo com o resistor de , eles possuem a mesma tensão.

Agora, vamos escrever a corrente em função da tensão nodal .

Substituindo,

Como,

Substituindo,

Chegamos a uma EDO não homogênea. A solução geral dessa equação é composta pela solução particular mais a solução da homogênea.

Primeiro, vamos resolver a homogênea:

Nós já resolvemos essa EDO quando estudamos o caso sem fontes e vimos que resposta é:

Agora, precisamos encontrar a solução particular.

Como é uma constante, a solução particular deve ser também uma constante:

sendo uma constante.

Substituindo, temos:

Como a derivada de uma constante é zero:

Portanto, a solução geral é:

Agora, precisamos encontrar o valor da constante Até o instante , não há circulação de corrente no circuito. Logo, . Lembrando que a corrente no indutor não pode variar instantaneamente, então:

Então, utilizando a nossa condição inicial

Substituindo:

Logo, a corrente no indutor para será:

Agora temos que calcular para .

Como a tensão da fonte passa a ser zero para , a fonte de tensão pode ser substituída por um curto-circuito, tornando o circuito igual ao caso sem fonte.

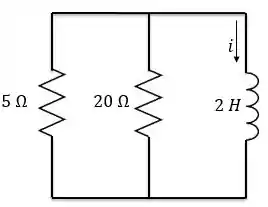
Fazendo a associação em paralelo dos resistores, temos:

Chegando nesse circuito RL sem fonte simples.

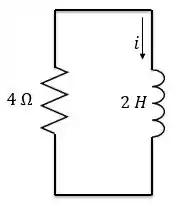
Aqui a gente tem que ter um cuidado especial, pois a nossa condição inicial é em Então, temos que considerar esse deslocamento no tempo.

Como a corrente no indutor não pode variar instantaneamente, ou seja:

Para instante , temos a expressão da corrente, que foi aquele calculado em Logo:

Logo, a corrente no indutor para será: