Para o circuito da figura, composto de valores padrão:
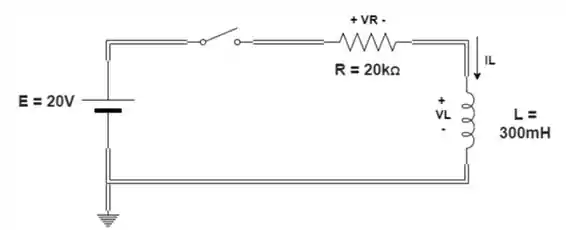
- Determine a constante de tempo.
- Escreva a expressão matemática para a corrente após a chave ser fechada.
- Repita o item (b) para e .
- Determine e em uma, três e cinco constantes de tempo.
Passo 1
A constante de tempo para o circuito RL é dada pela fórmula:
Passo 2
Após a chave ser fechada, no caso do indutor, a corrente irá aumentar de acordo com a fórmula:
Passo 3
Vamos calcular a tensão no indutor após o fechamento da chave, ela irá decrescer ao longo do tempo:
Passo 4
Se a tensão do indutor está decrescendo, a tensão no resistor irá aumentar ao longo do tempo:
Passo 5
Vamos calcular e segundo as seguintes equações:
Para :
Para :
Para :
Resposta
a)
b)
c)
d)
Para :
Para :
Para :