Determine para e no circuito abaixo.
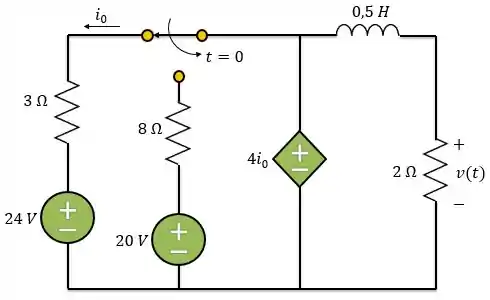
Passo 1
Vamos começar! Nesse circuito temos uma chave. Em essa chave muda de posição, ou seja, para a chave está na posição horizontal como está desenhado no circuito acima. Já para a chave muda de posição e se conecta com o resistor de .
Passo 2
Vamos encontrar a tensão , que é aplicada no indutor nesses dois casos.
Primeiro, vamos calcular a tensão para . Neste caso o circuito pode ser redesenhado assim:
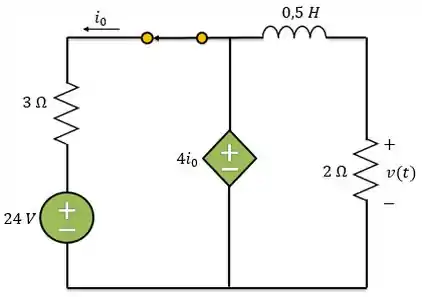
Considerando que o circuito estava funcionando no regime permanente. Sabemos que o indutor é um curto-circuito em corrente contínua.
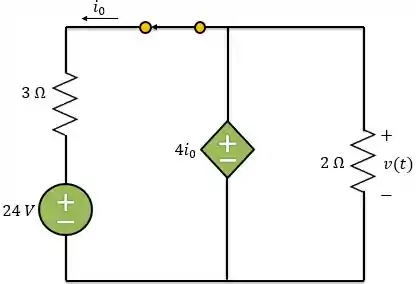
Logo, a tensão para , tem o valor da fonte de tensão dependente, já que a fonte está em paralelo com o resistor de .
Passo 3
Precisamos, então, descobrir o valor de . Aplicando a LTK na malha da esquerda do circuito acima, temos:
Logo,
Encontramos o valor da tensão, mas antes de analisarmos o circuito para vamos calcular a corrente que passa pelo indutor e pelo resistor de . Esse resultado vai nos ajudar ali na frente.
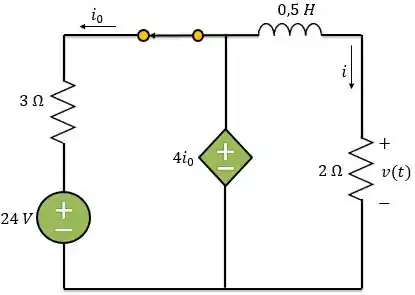
Pela lei de Ohm
Passo 4
Agora vamos analisar o circuito para . Para este caso, podemos considerar fonte dependente de tensão desligada, ou seja, um curto-circuito. Pois essa fonte depende de e esta corrente é zero para este caso.
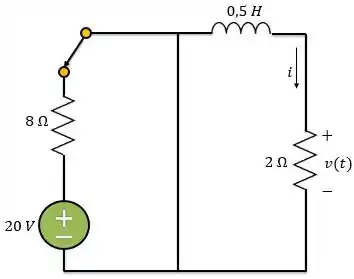
Devido a esse curto-circuito, o circuito a cima pode ser dividido em dois, como queremos encontrar , vamos analisar o lado direito do circuito.
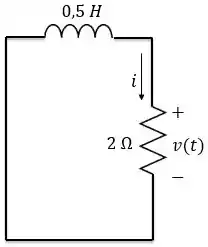
Esse circuito a gente conhece. É o circuito RL sem fonte. Sabemos que a corrente nesse circuito se comporta assim:
Passo 5
Nós temos os valores de e , precisamos só encontrar o valor da corrente no instante . Para isso, temos que lembrar que a corrente no indutor não pode variar instantaneamente.
Em a chave está na iminência de mudar de posição, mas ainda está aberta. Logo, o valor da corrente nesse instante é o mesmo de .
Logo,
Substituindo todos os valores que temos, chegamos a seguinte corrente para
Agora é só aplicar a lei de Ohm para encontrarmos a tensão para .