Exercícios Resolvidos de Classificação de Formas Quadráticas

Exercício 5 1 2 3 4 6 7 8 9 10

Enunciado

USP, Sem Campus, Álgebra Linear 2, Psub - 2017, Questão 1

Seja fixado um sistema de coordenadas no espaço, com uma

base ortonormal, e considere a quádrica de equação:

. Sabendo-se que , em que

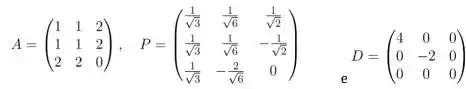
temos que uma equação reduzida para essa quádrica é:

Passo 1

Fala pessoal, tudo beleza? Vamos para mais uma questão de Algelin. Nosso objetivo é descobrir qual qual é a equação reduzida da quádrica

Bora resolver essa questão!!!

A primeira coisa que precisamos fazer é escrever a equação da quádrica utilizando matrizes. Fazendo isso, a nossa equação fica

Passo 2

Agora, vamos fazer a seguinte transformação.

substituindo na nossa equação

temos:

Usando o fato que , e que como é ortogonal então . então

Lembrando que

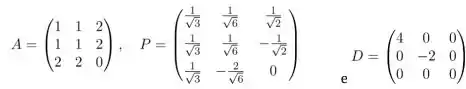
Então, ao realizar esse produto. Temos.

Passo 3

Chegamos a conclusão que

é a equação reduzida da cônica

Prontinho pessoal!! Finalizamos mais uma questão. Espero que os passos tenham ficado claros. Até a próxima questão e bons estudos!!!! 😊

Resposta

Exercícios de Livros Relacionados

Encontre uma fórmula para a forma quadrática que não utilize matrizes. x y ⋅ 2 - 3 - 3 5 ⋅ x y

Escreva a equação quadrática na notação matricial x T A x + K x + f = 0 , onde x T A x é a forma quadrática associada e K é uma matriz apropriada. a2 x 2 + x y + x - 6 y + 2 = 0 by 2 + 7 x - 8 y - 5 =

Identifique o tipo de cônica representada pela equação a4 x 2 + 9 y 2 = 1 b4 x 2 - 5 y 2 = 2 0 c - x 2 = 2 y dx 2 - 3 = - y 2

Identifique o tipo de cônica representada pela equação a2 x 2 + 5 y 2 = 20 bx 2 - y 2 - 8 = 0 c7 y 2 - 2 x = 0 dx 2 + y 2 - 25 = 0

Encontre uma matriz 3×3 simétrica cujos autovalores sejam λ 1 =- 1 ,λ 2 =3 ,λ 3 =7 e os autovetores associados sejam v 1 =( 0 ,1 ,- 1 ) , v 2 =1 ,0 ,0 ,v 3 =( 0 ,1 ,1 ) .Existe uma matriz 3×3 simétric