Abaixo é dado um paralelepípedo de concreto submetido aos carregamentos mostrados na figura. Sabendo que , de termine a deformação em mm de cada lado do paralelepípedo.
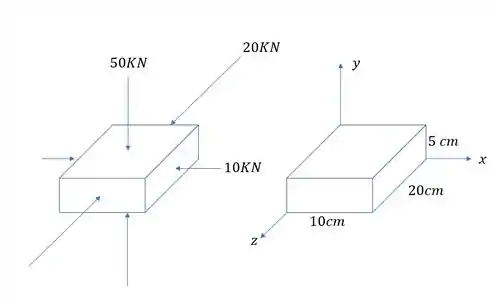
Passo 1
Esse problema se trata de um problema em que temos que usar a fórmula de deformação nos eixos. A fórmula que temos que usar é a fórmula da lei generalizada de Hooke que é dada por
Outro cuidado que temos que tomar é que essas fórmulas dão a deformação especifica em cada eixo, e o enunciado pede a de formação total, ou seja, precisaremos saber que a relação entre deformação especifica e total é dada por
Como o objetivo é determinar a deformação total podemos escrever essa fórmula como
Agora que já definimos quais fórmulas usar, devemos determinar cada parte da fórmula.
Passo 2
Vamos primeiro determinar as tensões em cada um dos eixos. Sabemos que a fórmula que nos dá as tensões em cada eixo é
Vale prestar atenção que todas as cargas aplicadas na nossa peça são cargas de compressão, logo todos os normais devem possuir sinal de menos. Com isso teremos que
Também precisamos determinar as áreas relativas a cada um dos normais.
Agora é fácil determinar o valor das tensões em cada face do nosso paralelepípedo
Passo 3
Já com as tensões em mãos basta determinar as deformações especificas, tomando, é claro, cuidado com os sinais que determinamos, logo teremos que
Em que
Substituindo teremos que
Passo 4
Como eu disse é pedido a deformação total e não especifica, ou seja, temos que usa a seguinte fórmula.
Nos foi pedido também a deformação em mm, logo temos que garantir que esses comprimentos estarão corretor também, logo teremos que.
Substituindo teremos que
Com isso podemos deduzir que os eixos y e z sofreram compressão enquanto que o eixo x sofrerá uma expansão, mesmo atuando no eixo x uma carga de compressão.
Isso ocorre pois as deformações nos eixos y e z são maiores que as deformações de compressão em x, obrigando, nesse caso, o eixo x expandir.