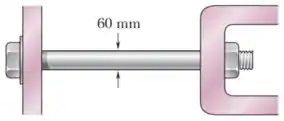
Exercícios Resolvidos de Coeficiente de Poisson

Enunciado

A variação no diâmetro de um grande parafuso de aço é cuidadosamente medida enquanto a porca é apertada. Sabendo que e , determine a força interna no parafuso, quando se observa que o diâmetro diminuiu em .

Passo 1

O que está acontecendo?

Ao mesmo tempo que o parafuso faz forças nas peças rosas para manter elas em suas posições, as peças reagem tracionando o parafuso pelas extremidades.

Essa tração significa que existe no parafuso uma força interna normal e uma tensão normal média:

Pela Lei de Hooke, essa tensão corresponde a uma deformação normal/longitudinal no parafuso:

E pela definição do coeficiente de Poisson , essa deformação longitudinal é acompanhada por uma deformação lateral :

Agora, o exercício disse que o parafuso tinha um diâmetro inicial e sofreu uma diminuição de , ou seja, ele sofreu uma variação de diâmetro .

Isso significa que o exercício nos descreveu a variação lateral no parafuso, uma vez que:

E o que é que o exercício quer?

Ele quer saber o valor da força interna normal no parafuso.

Para descobrir esse valor, vamos partir da fórmula da tensão normal média e desenvolver ela usando a Lei de Hooke, a definição do Coeficiente de Poisson e a definição da deformação lateral.

Dessa forma, vamos conseguir descrever a força a partir de valores que conhecemos, como:

O módulo de elasticidade ;
O coeficiente de Poisson ;
O diâmetro inicial ;
E a variação de diâmetro .

Passo 2

Então primeiro, vamos resolver o exercício literalmente. Em seguida, substituímos os valores e encontramos .

Partindo da fórmula da tensão normal média, temos:

Queremos encontrar , então podemos isolá-lo desde já:

Ok!

Agora, a tensão pode ser descrita pela Lei de Hooke .

E a área da seção transversal do parafuso é circular e pode ser descrita em função de seu diâmetro através da fórmula .

Fazendo essas substituições, temos:

Arrumando a expressão, ela fica assim:

Beleza...

Conhecemos os valores de e , mas não conhecemos o valor da deformação longitudinal .

Mas sabemos descrever a deformação lateral , e sabemos que essas deformações são relacionadas pelo coeficiente de Poisson:

Isolando , temos:

Substituindo isso na última expressão que tínhamos encontrado para :

Arrumando, fica assim:

Agora só falta descrever a deformação lateral .

Ela é a razão entre a variação de uma medida no sentido lateral (como o nosso diâmetro) sobre o valor inicial da medida, ou seja:

Fazendo essa última substituição, a força fica assim:

Simplificando, temos:

Passo 3

Agora, só falta substituir os valores de , , e na expressão que encontramos para :

Fazendo as substituições:

Pausa para olhar para as unidades...

é o mesmo que .

Então se a gente conseguir reescrever a variação de (micrometros) em milímetros (), as unidades de milímetros vão se cortar e o resultado para a força vai sair em .