Um tubo de aço de comprimento igual a , diâmetro externo de e espessura de parede de é usado como uma coluna curta e suporta uma força axial centrada de .
Sabendo que e , determine a variação no comprimento do tubo, a variação em seu diâmetro externo e a variação na espessura da parede.
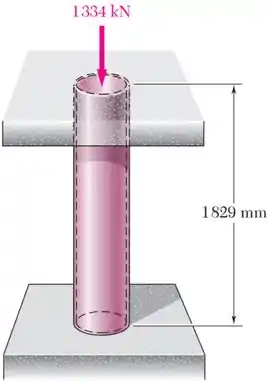
Passo 1
O tubo tem, inicialmente, um comprimento , um diâmetro externo e uma parede de espessura .
Além disso, o tubo é feito de um aço de módulo de elasticidade e Coeficiente de Poisson .
Quando o tubo for carregado com a força de compressão de , vai surgir nele uma força interna normal , que vai gerar nele uma tensão normal média .
De acordo com a Lei de Hooke e o Coeficiente de Poisson, essa tensão normal no tubo vai ser acompanhada por deformações longitudinal e lateral .
E o que é que o exercício quer?
Ele quer que a gente determine as variações de comprimento , de diâmetro externo e de espessura da parede no tubo quando ele é carregado com a força de .
Para encontrar a variação de comprimento do tubo no item , podemos usar a fórmula que vem da combinação da Lei de Hooke com as fórmulas da tensão normal média e da deformação normal:
Já para encontrar as variações do diâmetro externo e da espessura da parede nos itens e , vamos precisar nos lembrar da definição de deformação lateral:
A deformação lateral é definida como a variação de uma medida no sentido lateral (como o diâmetro ou a espessura do tubo) sobre o valor inicial dessa medida.
Ou seja:
Então se conseguimos usar o Coeficiente de Poisson para encontrar , vamos conseguir encontrar em seguida e .
Passo 2
Vamos começar resolvendo o item .
Aplicando a fórmula que descreve a variação de comprimento de uma peça a partir do carregamento axial na peça, temos:
Sabemos que , e , mas não sabemos o valor da área da seção transversal do tubo.
Então vamos olhar para a seção transversal do tubo para encontrar sua área :
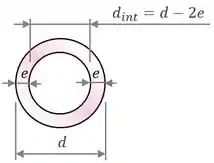
Vemos que dá pra definir a área como a diferença entre a área do círculo de diâmetro externo e a área do círculo de diâmetro interno .
A área de cada um desses círculos vai ser dada pela fórmula , então:
Colocando em evidência, encontramos que:
Podemos deixar essa área em função do diâmetro interno uma vez que pode ser calculado facilmente:
Passo 3
Encontrada uma expressão para a área , podemos substituir ela na fórmula :
Arrumando tudo, isso fica assim:
Agora, só falta substituir os valores de , , , e para encontra o valor da variação de comprimento sofrida pelo tubo.
Fazendo todas essas substituições, temos:
Como , as unidades e nessa equação vão se cortar, e o resultado final vai sair em milímetros ().
Calculando tudo, encontramos:
Que é a resposta do item !
Passo 4
Agora, antes de resolver os itens e , vamos encontrar a deformação lateral no tubo, já que é ela que descreve as variações do diâmetro externo e da espessura da parede .
A deformação lateral aparece na fórmula do Coeficiente de Poisson, então vamos começar usando essa fórmula:
Isolando a deformação lateral , temos:
Como a deformação longitudinal é definida como a variação de comprimento sobre o comprimento original , temos que:
Conhecemos , e , então encontramos a deformação lateral no tubo!
Passo 5
No passo anterior, encontramos que:
Agora, podemos usar isso para resolver os itens e .
Começando pelo item ...
Queremos encontrar a variação do diâmetro externo , então definimos a deformação lateral como:
Substituindo isso na expressão que encontramos no passo anterior, temos que:
Isolando :
Inserindo os valores de , , e :
O que dá:
Ou se preferirmos:
Passo 6
Finalmente, para o item , repetimos o que fizemos para o item :
Queremos encontrar a variação da espessura da parede , então definimos como:
Substituindo isso na expressão do passo anterior, temos que:
Inserindo os valores de , , e , encontramos a variação da espessura da parede :
Ou em notação científica: