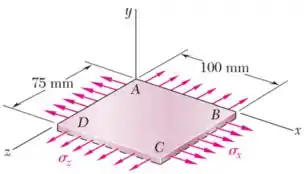
Um tecido utilizado em estruturas infláveis está submetido a um carregamento biaxial que resulta em tensões normais e . Sabendo que as propriedades do tecido podem ser de aproximadamente e , determine a variação no comprimento do lado , do lado e da diagonal .
Passo 1
Nos exercícios anteriores, a gente sempre trabalhou com só uma tensão normal e com as deformações longitudinal e lateral .
Agora, nesse exercício, nós temos tensões multiaxiais:
- No eixo , temos uma tensão normal ;
- No eixo , não temos tensão normal, então ;
- E no eixo , temos uma tensão normal .
Por esse motivo, ao invés de usarmos as deformações longitudinal e lateral em exercícios como esse, usamos as deformações em cada eixo: , e .
E como a gente encontra essas deformações em cada eixo?
Lembra aí!
Existem fórmulas para as deformações em cada eixo como consequência das tensões multiaxiais:
Cada uma dessas fórmulas é o resultado da soma dos efeitos que as tensões em cada eixo têm na deformação em uma certa direção.
Beleza, e o que é que o exercício quer?
Ele quer saber:
A variação no comprimento do lado , .
Como o lado está ao longo do eixo , essa variação vai ser definida pela deformação em :
onde é o comprimento inicial de do lado .
A variação no comprimento do lado , .
está ao longo do eixo , então:
Onde é o comprimento inicial de do lado .
A variação no comprimento da diagonal , .
Não existe uma “deformação diagonal” que define a variação de , mas podemos pensar nessa variação assim:
Inicialmente, a diagonal tem um comprimento que pode ser encontrado a partir do Teorema de Pitágoras:
Enquanto que, ao final, o lado vai ter um comprimento e o lado um comprimento , de tal forma que a diagonal vai ter um comprimento final :
E assim a variação vai ser dada por:
Então, resumindo...
Se encontramos as deformações em e em ( e ), vamos poder calcular as variações e , resolvendo os itens e .
E, conhecendo as variações e , conseguimos calcular a variação da diagonal, , resolvendo assim o item .
O material tem um módulo de elasticidade e um coeficiente de Poisson .
Passo 2
Então vamos começar o exercício encontrando as deformações em e em ( e ).
Usando as fórmulas para a deformação em e em em situações de tensões multiaxiais, temos:
Como, no nosso caso, a tensão normal em é igual a zero, temos que:
O exercício nos forneceu o valor do módulo de elasticidade em , sendo que as tensões e foram fornecidas em .
Para que os nossos resultados de deformação sejam adimensionais, vamos reescrever o módulo de elasticidade em na hora de substituir o seu valor.
Substituindo os valores de , , e , temos:
Calculando tudo, encontramos:
Passo 3
Agora que sabemos as deformações em e em , podemos resolver os itens e .
Começando pelo item :
Podemos definir a deformação em como:
Como queremos encontrar no item a variação do comprimento do lado , devemos isolar :
Substituindo os valores de e , temos:
O que dá:
Passo 4
E agora para o item :
Queremos encontrar a variação do comprimento do lado , que é descrita pela deformação em :
Isolando , temos:
Substituindo os valores de e :
O que dá:
Passo 5
Por último, resolvemos o item :
Queremos encontrar a variação de comprimento da diagonal .
Toda variação de comprimento é igual ao comprimento final menos o comprimento inicial, logo:
O comprimento inicial pode ser encontrado através do Teorema de Pitágoras, usando os lados e como os catetos e o lado como a hipotenusa:
Da mesma forma, o comprimento final também pode ser calculado através do Teorema de Pitágoras.
Mas, dessa vez, os lados e vão ter seus comprimentos finais, que vão ser iguais aos seus comprimentos iniciais mais as variações de comprimento sofridas:
Dessa forma, temos que:
Substituindo todos os valores, temos:
O que dá: