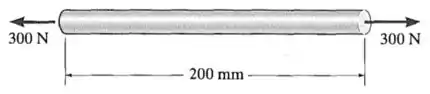
A haste plástica de acrílico tem de comprimento e de diâmetro. Se uma carga axial de for aplicada a ela, determine a mudança em seu comprimento e em seu diâmetro.
, 0.
Passo 1
O exercício quer saber a variação do comprimento (tradicionalmente chamada de ) e a variação do diâmetro da haste.
Para encontrar a variação do comprimento, podemos nos lembrar da fórmula que obtemos quando combinamos a Lei de Hooke () com as fórmulas da tensão normal média () e da deformação normal ():
Com essa fórmula, conseguimos calcular a variação do comprimento da haste a partir:
- Da força interna normal , que vai ser igual à carga de tração de ;
- Do comprimento inicial da haste;
- Do módulo de elasticidade do plástico;
- E da área da seção transversal da haste, que pode ser descrita em função de seu diâmetro através da fórmula .
Agora, essa haste não vai sofrer deformação só no sentido longitudinal (sentido do seu comprimento). Ela também vai se deformar no sentido lateral (sentido do seu diâmetro).
O coeficiente de Poisson do plástico vai ditar a razão entre essas deformações e através da fórmula:
A deformação no sentido longitudinal pode ser calculada dividindo a variação do comprimento nesse sentido pelo comprimento original :
Enquanto isso, a deformação no sentido lateral é a divisão da variação de uma medida no sentido lateral pelo valor inicial dessa medida.
Usando o diâmetro como essa medida, temos:
Usando essas três últimas fórmula, vamos poder calcular a variação do diâmetro da haste.
Passo 2
Vamos começar encontrando a variação do comprimento da haste.
Combinando a Lei de Hooke () com as fórmulas da tensão normal média () e da deformação normal (), temos:
Como a área da seção transversal dessa haste é circular, ela pode ser descrita em função de seu diâmetro através da fórmula :
Substituindo os valores , , e :
Reescrevendo como , temos:
Como , as unidades “” e “” nessa equação vão se cortar e o resultado vai sair em milímetros ().
Calculando tudo, encontramos:
Metade do exercício já está resolvido, agora vamos para a próxima metade!
Passo 3
Queremos encontrar a variação do diâmetro da haste.
Da equação do coeficiente de Poisson, temos:
Onde:
Substituindo essas definições na equação do coeficiente de Poisson:
Isolando nessa expressão, encontramos:
Substituindo os valores de , , e :
Calculando tudo, isso dá:
E assim temos as respostas para o exercício: