Elementos da linguagem e da lógica matemáticas
Considere a seguinte proposição:
- Decida se a proposição é verdadeira ou falsa
- Enuncie a recíproca e decida se a mesma é verdadeira ou falsa;
Passo 1
Vamos lá! Começar descobrindo o conjunto solução da hipótese e depois verificar se está contido no conjunto solução da tese! Repare que são duas inequações, vamos começar analisando a inequação da hipótese.
Isso nos diz que
Ou seja
Concluímos, então, que o conjunto solução para a hipótese é .
E agora repare que o conjunto solução da tese não está explícito em forma de um intervalo. Isso significa que teremos que encontrar essa solução também. Vamos lá!
Passo 2
Aqui não podemos multiplicar cruzado como fazemos com a igualdade, temos que achar a fração e analisar o seu sinal.
Vamos analisar os sinais desses caras, para isso vamos usar o quadro de sinais
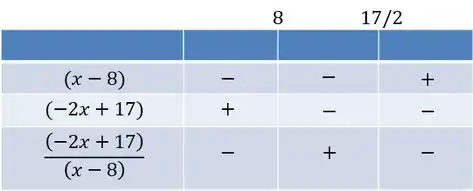
Como ele quer a parte positiva o intervalo que é o resultado dessa inequação vai ser
Passo 3
Com os dois conjuntos solução em mãos, basta analisarmos se a hipótese está contida na tese.
Podemos concluir que há valores de na hipótese que NÃO pertencem ao conjunto solução da tese. Como por exemplo: . E portanto a proposição é FALSA!
Passo 4
O enunciado da recíproca é simples! Basta invertermos os papéis de hipótese e tese:
E para dizermos se é verdadeira ou falsa, basta analisarmos se a hipótese está contida na tese, lembrando que agora trocamos os papéis de hipótese e tese!! Dessa vez temos que ver se está contido em , podemos perceber que TODO valor de à é maior que , logo está contido em e a recíproca é verdadeira
Resposta
- Falso
- Verdadeiro