
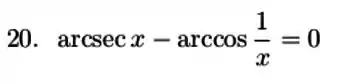
Passo 1
Temos
Isso é a mesma coisa que
E, se chamarmos de , vamos ter que
Assim
Passo 2
Isolando o cosseno,
Substituindo isso no lado direito da nossa equação, ficamos com
Agora, qual é o arco cujo cosseno é cosseno de ?
É o próprio , né?
Então
Passo 3
Então, no passo 1 dissemos que
E no passo 2 achamos que
Substituindo tudo isso na equação que quermos provar
Provamos que
Fim de papo.
Resposta
Ei, a resposta está no passo a passo :)