
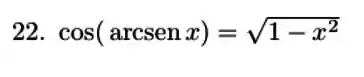
Passo 1
Vamos lá. Uma função dentro do cosseno parece um pouco estranho, né!?
Então vamos chamar essa função de , assim
E então ficamos com
Passo 2
Ótimo, agora que já deixamos nossa função com um acara um pouco mais agradável (sem função dentro de função), vamos voltar a primeira relação que achamos
Se isso é verdade, então
A gente não é Ana Maria Braga, mas vamos reservar isso um pouquinho, pra usar depois.
Passo 3
Adivinha o que vamos usar agora?
Aquilo que a gente quase sempre usa quando temos seno e cosseno.
Isso mesmo, a relação fundamental da trigonimetria!!
Isolando o cosseno, ficamos com
Passo 4
E aí, já tá vendo onde eu quero chegar?
No passo 2 a gente achou que
Substituindo isso na equação do cosseno que acabamos de achar, temos que
E, se considerarmos
Temos que nesse intervalo, , então
E quem era mesmo?
Assim, provamos que
Resposta
Ei, a resposta está no passo a passo :)