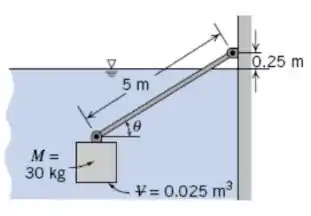
Um bloco de massa e volume está imerso na água, conforme mostrado. Um tirante de seção circular de de comprimento e de seção transversal está preso ao bloco e também à parede. Se a massa do tirante é de , qual será o ângulo para o equilíbrio?

A primeira pergunta é no que o ângulo vai influenciar na questão?

Ele vai influenciar em quanto do tirante está na água, influenciando assim no empuxo.

Então nosso primeiro passo é descobrir o empuxo que fará com que o sistema esteja em equilíbrio.

Para isso precisamos saber as forças atuantes. No bloco teremos peso e empuxo e no tirante também.

Então vamos começar pelo bloco. O peso é:

E o empuxo será:

Assim, no bloco teremos uma força resultante atuando na direção do peso, isto é, para baixo:

O ponto de atuação será na extremidade do tirante.

Agora vamos calcular a força peso do tirante.

Atuando na metade do tirante, a uma distância de da parede.

Beleza, sabemos que a empuxo devido ao tirante vai atuar no meio da parte submersa, temos o seguinte sistema de forças:

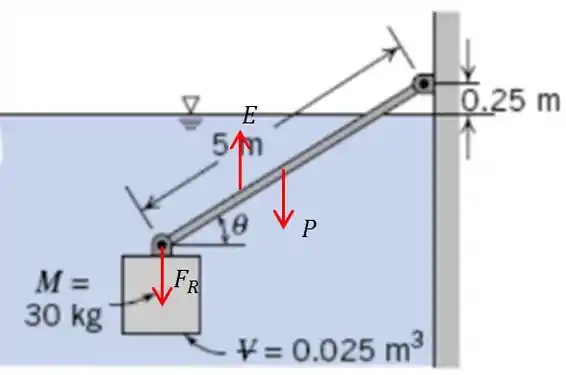
O nosso problema todo é o empuxo que depende de . Pois esse ângulo vai influenciar no quanto do tirante está fora da água.

Sendo assim, vamos chamar a parte fora da água de , e ela depende de . Olha a imagem abaixo:

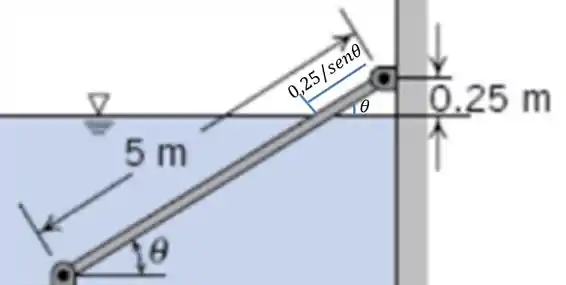
Pelo triângulo, temos que:

Chamando de a parte fora da água, o volume submerso será:

Assim o empuxo será:

E o ponto de aplicação do empuxo será, na metade do volume submerso, sendo assim na posição:

Mas para o momento a gente quer a distância do centro de carena até o pino lá na parede e por isso precisamos somar a parte fora da água, :

Beleza, agora conseguimos montar a equação de momento:

Em que é a força resultante no bloco.

Multiplicamos por porque precisamos das distâncias horizontais.

Simplificando o que podemos chegamos em:

Assim, voltando lá na equação em que relacionamos a distância com o ângulo