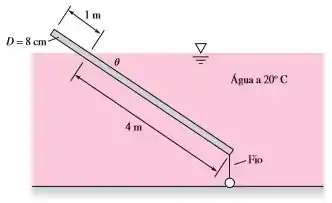
A haste de madeira redonda uniforme de de comprimento da Figura abaixo está presa ao fundo por um fio. Determine a tração no fio e a densidade da madeira. É possível, com as informações dadas, determinar o ângulo de inclinação ? Explique.
Passo 1
A haste sofre a ação da força peso em seu centro de gravidade; do empuxo no centro de carena; da força de tensão do fio.
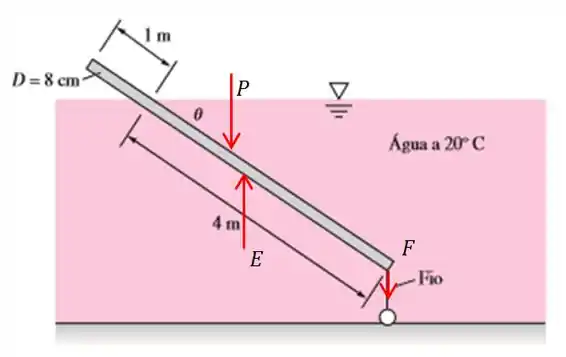
Como a haste está presa somente ao fio, vamos fazer o momento em relação a este ponto, que seria o ponto de giro da haste.
Mas antes disso temos que saber a posição do centro de gravidade e de carena.
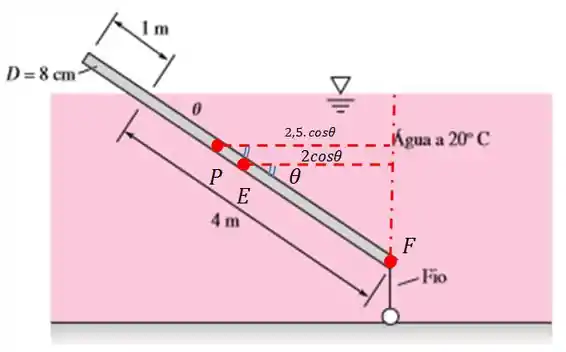
O centro de gravidade é na metade da barra, assim a da extremidade com o fio. Já o centro de carena é na metade do volume submerso sendo assim a da extremidade do fio.
Agora podemos montar a equação de momento em relação ao ponto de contato da haste com o fio. Como temos equilíbrio então o momento total deve ser zero:
Mas, pera! Momento é força vezes braço, onde a força é perpendicular ao braço. E não é o que tá acontecendo aqui!
Sim, por isso vamos ter que multiplicar a distância entre o ponto de aplicação e a extremidade do fio pelo cosseno de Vamos projetar o braço horizontal.
Beleza, sabemos como o peso e o empuxo vão se relacionar. Então se soubermos um deles, encontramos o outro. Não conseguimos descobrir o peso da haste sem a densidade da madeira.
Mas o empuxo a gente consegue descobrir.
Sendo assim:
Pela imagem vemos que da haste está submerso, já que metros de estão submersos. O comprimento total é . Sendo assim do volume da haste está submersa.
E o empuxo fica assim:
Calculando o volume da haste
Assim, o empuxo será:
Agora sabemos o valor do peso:
Podemos então calcular a força em de tensão, como o sistema está em equilíbrio o somatório de forças deve ser zero, assim:
Passo 2
Tendo o peso da haste podemos calcular a densidade dela, já que sabemos seu volume
Sobre o ele é irrelevante na questão, pois no momento ele se cancela, mostrando que a inclinação da haste não interfere. Sendo assim não conseguimos calculá-lo.