Um cubo, cujas arestas medem , é feito de um material de espuma rigido e flutua em água com abaixo da superfície. Calcule a magnitude e a direção da força requerida para mantê-lo completamente submerso em glicerina, cuja gravidade específica é 1,26.
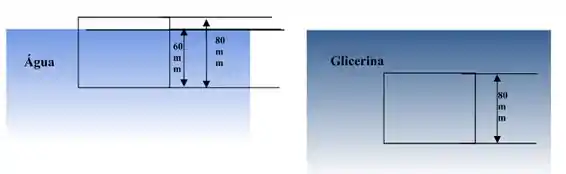
Passo 1
Temos dois casos, o caso em que o cubo é mergulhado na água e posteriormente o caso que é mergulhado em glicerina.
Vamos começar obtendo os dados necessários com o primeiro caso, onde sabemos que o sistema está em equilíbrio.
Se está em equilíbrio temos que
O peso do cubo será:
O empuxo por sua vez, será:
Agora igualando as equações
Passo 2
Agora que descobrimos o que faltava das informações do cubo podemos analisar o segundo caso. Onde para atingirmos o equilíbrio o sistema disse que será necessária uma força .
Vamos supor que a força , esteja atuando para baixo junto com o peso.
Então para montar o sistema de equilíbrio de forças teremos:
Beleza, o peso a gente já calculou:
O empuxo será:
Lembrando que gravidade especifica é só uma outra forma de falar densidade relativa, então temos que a densidade da glicerina é:
Como o cubo está todo submerso o volume submerso é o volume total do cubo
Voltando a equação de forças temos:
Como encontramos um valor positivo significa que acertamos nosso chute a força atua no mesmo sentido da força peso.