A esfera mostrada na figura abaixo possui um volume de e flutua na água, como pode ser observado. Determine seu peso específico.
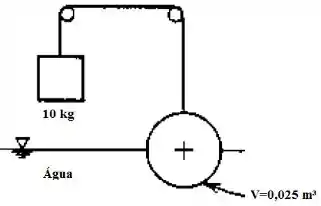
Passo 1
O sistema está em equilíbrio, sendo assim o somatório de forças é zero.
A esfera sofre a ação do empuxo, da força de tração que equilibra o peso de e do peso da esfera.
E lembrando que peso é , a equação de forças é:
Passo 2
Agora vamos ver o que podemos substituir nessa equação pra resolver ela.
O empuxo exercido na esfera é proporcional ao volume submerso. Pela imagem, metade do volume total da esfera. Sendo assim temos:
Podemos cortar a gravidade, substituir o volume e chegamos em:
Passo 3
Show! Mas a questão pede o peso específico, e não a massa específica da esfera.
A relação entre o peso específico () e a massa específica () é:
Isso aí. Só precisamos multiplicar pela gravidade então: