Um cubo, de de aresta, tem sua metade inferior de densidade relativa igual a e a metade superior igual a . Está submerso na massa de dois fluidos imiscíveis, o inferior de densidade relativa igual a e o superior de . Determinar a altura do cubo que sobressai por cima da interface dos dois líquidos.
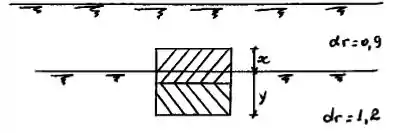
Passo 1
Questão louca com dois fluidos e um objeto composto por dois materiais.
O primeiro passo é calcular o peso do objeto.
Como ele é feito metade de um material e metade de outro, vamos tratar de dois objetos de volume . Onde
Então calculando o peso da parte inferior cujo material tem densidade de
O peso da parte de cima cujo material tem densidade
Assim o peso total do objeto é:
Passo 2
Agora que sabemos o peso do objeto podemos montar a equação de equilíbrio de forças.
Teremos a ação da força peso para baixo, e de dois empuxo empurrando o objeto para cima. Assim formando o equilíbrio.
O empuxo um é o empuxo devido ao liquido de densidade . O volume de liquido deslocado vai depender da porção submersa, chamaremos de , assim como fez o desenho do enunciado.
Já o empuxo devido ao fluido de densidade será:
Sendo a porção submersa pelo fluido .
Jogando todos os resultados que tivemos na equação de equilíbrio que montamos nesse passo, temos:
Como o cubo não mudou de tamanho se somarmos as partes submersas por cada fluido elas juntas deve dar o tamanho da aresta do cubo, sendo assim:
Assim, podemos substituir que:
Isolando , temos:
Assim,