Aletas em forma de pino são amplamente utilizadas em sistemas eletrônicos para promover resfriamento, bem como suporte de componentes. Considere uma aleta em forma de pino de diâmetro uniforme , comprimento e condutividade térmica conectando dois componentes de comprimento e área de superfície . Os componentes são caracterizados por uma geração volumétrica de energia térmica e condutividade térmica . Considere que as superfícies expostas dos componentes estão a uma temperatura uniforme correspondente àquela da base da aleta pino () e que o calor é transferido por convecção da superfície exposta para um fluido em contato. A parte posterior e as laterais dos componentes estão perfeitamente isoladas.
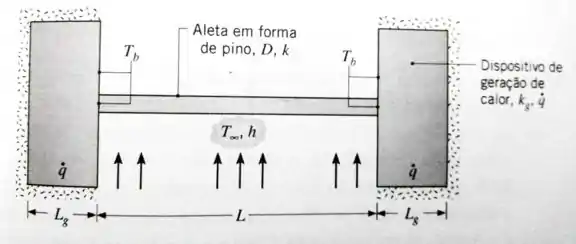
Deduza uma expressão para a temperatura da base em função dos parâmetros do componente (, , e ), dos parâmetros de convecção ( e ) e dos parâmetros da aleta (, e ).
Passo 1
Observamos que haverá troca de calor, por condução, no interior da aleta e, por convecção, nas superfícies dos componentes e da aleta.
Devido à simetria do problema, a gente pode resolver só um dos lados e afirmar que acontece o mesmo do lado oposto. Com isso, dizemos que as duas metades não trocam calor entre si e vamos usar as equações do caso B de aleta adiabática na extremidade:
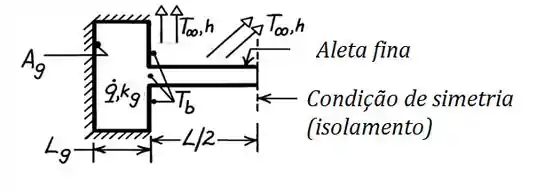
Essa estratégia é a mesma que fazemos com uma parede plana de condições de contorno simétricas.
Pelo balanço de energia na superfície de controle:
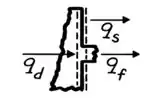
Então, a gente tem uma taxa de energia que entra (proveniente da geração de calor) e parte dessa energia sai pela aleta () e parte sai pela superfície lisa ():
Tudo que está entrando de energia nessa superfície () vem da geração volumétrica na parede. Então, a gente pode fazer um balanço de energia na parede pra expressar essa taxa de entrada ():
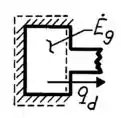
Em termos dos dados geométricos que temos, o volume pode ser reescrito:
Substituindo no balanço de superfície, a gente fica com:
Agora a gente precisa achar uma expressão para a taxa de calor que sai pela superfície plana () e a taxa de calor que sai pela aleta ()!
Passo 2
Bora determinar primeiro o mais fácil: a taxa de calor pela superfície lisa ()! Isso é simplesmente uma convecção sobre uma superfície, então a gente calcula pela lei de resfriamento de Newton:
Nesse caso a temperatura da superfície é a mesma da base () e a área de troca térmica da parede lisa será:
Substituindo os valores da aleta:
Logo:
Passo 3
Agora, a gente precisa calcular a taxa de calor da aleta!
A aleta em questão se enquadra no caso , então a taxa de calor perdida por ela pode ser escrita como:
Em que:
Bora calcular cada um deles então!
A área já foi calculada antes e o perímetro é dado por:
Logo:
E ainda:
Substituindo na expressão da taxa de calor da aleta:
Passo 4
Substituindo as expressões do calor trocado pela superfície plana () e pela aleta () no balanço de energia na superfície:
Isolando a temperatura da base ():