Dois longos bastões de cobre , com diâmetro , serão soldados pelas extremidades com uma solda com ponto de fusão de . Os bastões encontram-se em um ambiente a com um coeficiente de transferência de calor igual a .
Qual é a menor alimentação de potência necessária para efetuar a soldagem?
Passo 1
A ideia aqui é a seguinte:
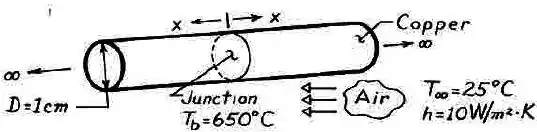
Como estamos tratando os dois bastões de cobre como longos, ambos correspondem ao Caso D da nossa tabela.
Assim, a taxa de transferência de calor necessária para manter a extremidade de cada bastão à temperatura de vai ser dada por:
Assim, como precisamos manter as das duas extremidades das duas à mesma temperatura, a quantidade mínima de potência necessária será:
Passo 2
Dados:
Substituindo os valores:
Resposta
Exercícios de Livros Relacionados
Um pino de área transversal uniforme é fabricado em uma liga de alumínio k=160 W m K . O diâmetro da aleta é D=4m m e ela está exposta a condições convectivas caracterizadas por h=220 W m 2 K . É info
Um dispositivo experimental para medir a condutividade térmica de materiais sólidos envolve o uso de dois bastões longos, equivalentes em todos os aspectos, exceto que um é fabricado com um material-p
A superfície de uma parede plana a 200 °C deve ser resfriada com aleta tipo pino de alumínio de perfil parabólico com ponta arredondada. Cada aleta tem comprimento de 25 mm e diâmetro de base de 4 mm.
Qual é a razão para o uso generalizado de aletas nas superfícies?
A intensidade na qual a condição na extremidade afeta o desempenho térmico de uma aleta depende da geometria da aleta e de sua condutividade térmica, assim como do coeficiente convectivo. Considere um