Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Equação da Aleta

Ver Teoria
Exercício 21345678

Enunciado

Bastões circulares de cobre k = 400   W / m K , com diâmetro D = 1   m m e comprimento L = 25   m m , são usados para aumentar a transferência de calor em uma superfície mantida a T x , 1 = 100 ° C .

Uma extremidade do bastão é presa a essa superfície (em x = 0 ), enquanto a outra extremidade ( x = 25   m m ) é conectada a uma segunda superfície, mantida a T x , 2 = 0 ° C . Ar, escoando entre as superfícies (e sobre os bastões), também se encontra a uma temperatura T ∞ = 0 ° C , mantendo um coeficiente convectivo h = 100   W / m 2 K .

a Qual é a taxa de transferência de calor por convecção entre um único bastão de cobre e o ar?

b Qual é a taxa total de transferência de calor dissipada de uma seção da superfície a 100 ° C com dimensões de 1 m por 1 m , se for instalado um feixe de bastões com distância entre os centros de 4   m m ?

Passo 1

a Qual é a taxa de transferência de calor por convecção entre um único bastão de cobre e o ar?

Vamos começar fazendo um balanço de energia nesse cara, a ideia é essa:

E ˙ e n t r a - E ˙ s a i = 0

q c o n d , i - q c o n d , o - q c o n v = 0

q c o n v = q c o n d , i - q c o n d , o

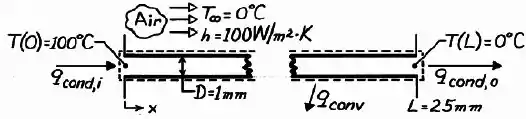
Opa! O problema está me falando que a temperatura na extremidade da barra é constante! Isso corresponde ao Caso C da tabela na Teoria!

Logo:

θ θ b = θ L / θ b sinh ⁡ m x + sinh ⁡ m L - x sinh ⁡ m L

Show de bola, vamos trabalhar nessa equação!

Passo 2

θ θ b = θ L / θ b sinh ⁡ m x + sinh ⁡ m L - x sinh ⁡ m L

Nessa equação, como T L = T ∞ :

θ L = T L - T ∞ = 0

Daí, podemos simplificar a equação:

θ θ b = sinh ⁡ m L - x sinh ⁡ m L

Onde:

sinh ⁡ t = e t - e - t 2

Logo:

θ θ b = e m L - x - e - m L - x e m L - e - m L

Agora é arrumar a bagunça:

θ θ b = e m L - m x - e - m L + m x e m L - e - m L

Multiplicando em cima e embaixo por e m L :

θ θ b = e 2 m L - m x - e m x e 2 m L - 1

Finalmente:

θ = θ b e 2 m L - m x - e m x e 2 m L - 1

Passo 3

Agora que encontramos como a temperatura varia ao longo de x , podemos calcular a taxa de transferência de calor por condução em função de x :

q c o n d = - k A c d θ d x = k A c θ b m e 2 m L - 1 e 2 m L - m x + e m x

No início e no final do bastão, a taxa de transferência de calor será:

q c o n d , i = q c o n d x = 0 = k A c θ b m e 2 m L - 1 e 2 m L + 1

q c o n d , o = q c o n d x = L = k A c θ b m e 2 m L - 1 2 e m L

Passo 4

Voltando para a expressão a taxa de transferência de calor por condução:

q c o n v = q c o n d , i - q c o n d , o

q c o n v = k A c θ b m e 2 m L - 1 e 2 m L + 1 - 2 e m L

Sendo m = h p / k A c :

q c o n v = h p k A c θ b e 2 m L - 1 e 2 m L + 1 - 2 e m L

Pra não embolar, vamos calcular cada coisa separadamente, ok?

h p k A c = h . π D . k . π D 2 4 = π 2 4 D 3 h k = π 2 4 × 10 - 3 3 × 100 × 400

h p k A c = 9,93 × 10 - 3

m = h p k A c = h π D k π D 2 / 4 = 4 h k D = 4 × 100 400 × 10 - 3

m = 31,62

θ b = T b - T ∞ = 100 ° C

Logo:

q c o n v = 9,93 × 10 - 3 × 100 e 2 × 31,62 × 0,025 - 1 e 2 × 31,62 × 0,025 + 1 - 2 e 31,62 × 0,025

q c o n v = 0,374   W

Passo 5

b Qual é a taxa total de transferência de calor dissipada de uma seção da superfície a 100 ° C com dimensões de 1 m por 1 m , se for instalado um feixe de bastões com distância entre os centros de 4   m m ?

Estando os bastões distantes de 4   m m   0,004   m entre seus centros, a quantidade de bastões que cabe em 1   m será:

1 0,004 = 250

Assim, no total, teremos:

N = 250 × 250 = 62500   b a s t õ e s

Dessa forma, a taxa total de transferência de calor será a soma da taxa de transferência por condução de cada bastão com a taxa de transferência por convecção da área não ocupada pelos bastões, logo:

q = N q c o n d , i + h A θ b

Onde:

q c o n d , i = k A c θ b m e 2 m L - 1 e 2 m L + 1 = 1,507   W

h = 100 W m 2 K

A = 1 m 2 - N A c = 1 - 62500 × π × 10 - 3 2 4

A = 0,951   m 2

θ b = 100 - 0 = 100   K

Logo:

q = 62500 × 1,507 + 100 × 0,951 × 100

q = 1,037 × 10 5   W

Resposta

a

q c o n v = 0,374   W

b

q = 1,037 × 10 5   W

Exercícios de Livros Relacionados

Um pino de área transversal uniforme é fabricado em uma liga de alumínio k=160 W m K . O diâmetro da aleta é D=4m m e ela está exposta a condições convectivas caracterizadas por h=220 W m 2 K . É info
Um dispositivo experimental para medir a condutividade térmica de materiais sólidos envolve o uso de dois bastões longos, equivalentes em todos os aspectos, exceto que um é fabricado com um material-p
A superfície de uma parede plana a 200 °C deve ser resfriada com aleta tipo pino de alumínio de perfil parabólico com ponta arredondada. Cada aleta tem comprimento de 25 mm e diâmetro de base de 4 mm.
Qual é a razão para o uso generalizado de aletas nas superfícies?
A intensidade na qual a condição na extremidade afeta o desempenho térmico de uma aleta depende da geometria da aleta e de sua condutividade térmica, assim como do coeficiente convectivo. Considere um