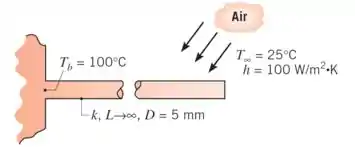
Uma barra circular longa de de diâmetro tem uma extremidade mantida a . A superfície da barra está exposta ao ar ambiente a com um coeficiente de transferência de calor por convecção de .
- Determinar a distribuição de temperatura ao longo da barra construída de cobre puro ().
- Qual a perda correspondente de calor a partir da barra?
- Estimar o comprimento da barra para que a hipótese de comprimento infinito forneça uma estimativa precisa para a perda de calor.
Passo 1
a) Pra gente determinar a distribuição de temperatura na aleta, a gente pode usar as equações que estão na tabela! A situação ilustrada pelo enunciado refere-se ao caso , pois o enunciado diz que a barra é longa.
Então, se a gente admitir que a barra tem comprimento infinito, sua superfície mais extrema terá a mesma temperatura que o fluido () e a equação do perfil de temperatura nessa situação será:
Ou seja:
A distribuição de temperatura é exatamente a expressão que descreve a temperatura ao longo de , então isolando o termo , a gente fica com:
Em que:
O termo é referente ao perímetro superfície mais extrema, ou seja, o perímetro da circunferência de diâmetro e o termo se refere à área dessa superfície!
Dessa maneira:
Logo:
Dessa maneira, a distribuição de temperatura na barra é dada por:
Passo 2
b) A gente pode obter a taxa de calor diretamente pela tabela também:
Substituindo os valores do enunciado:
Passo 3
c) Admitindo que a barra é muito longa, a temperatura da extremidade terá a mesma temperatura que o fluido, então ali não haverá perda de calor (não existe gradiente de temperatura).
E, se você der uma olhada na nossa tabela de fórmulas, você vai ver que existe uma expressão para a condição de superfície adiabática.
Nessa condição, a taxa de calor é dada por:
“Mas, se a superfície é adiabática, como que tem troca de calor?”. A extremidade é adiabática, mas o restante da superfície troca energia com o ambiente!
Como a gente quer que a taxa de calor no caso adiabático seja igual à taxa no caso de aleta de comprimento infinito, a gente poderia simplesmente igualar as expressões de cada um:
Essa equação só é satisfeita para tendendo ao infinito! Isso não é possível fisicamente! Então, o que a gente pode fazer é assumir que se a taxa chegar a do valor, isso já será suficiente! Bora ver no que dá então:
Essa equação é satisfeita para:
Como já calculamos o na letra a), a gente tem que:
Pronto! Esse é o comprimento da barra que a gente já pode considera-la infinita! Então, o comprimento pode ser maior ou igual a .