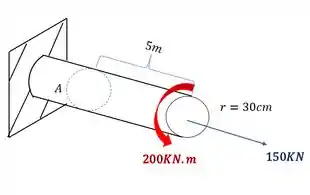
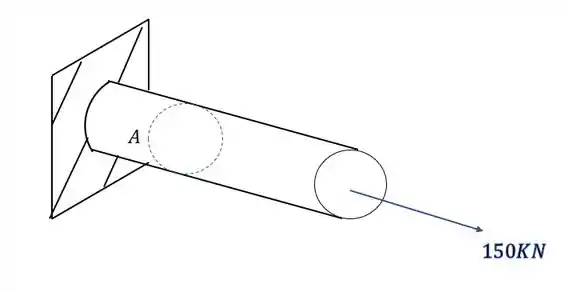
Abaixo foi dada uma barra sujeita a ação de um esforço torso, e um esforço normal. Sabendo disso determine o estado plano de tensões no ponto A que represente os esforços no mesmo.
Passo 1
Nesse tipo de questão, é sempre bom tomar extremo cuidado com as contas feitas. É muito importante fazer cada parte tomando extremo cuidado. Primeiro devemos levar todos os esforços do extremo da barra para o ponto que desejamos calcular, o desenho abaixo representa como vamos fazer isso.
Primeiro olhamos a seção que temos que levar os esforços
Em seguida analisamos quais solicitações os nossos esforços produziram
Sabemos que temos torção
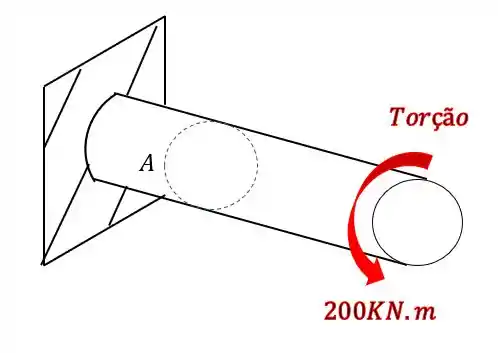
E temosNormal
Levando todos esses esforços para nossa seção, teremos que
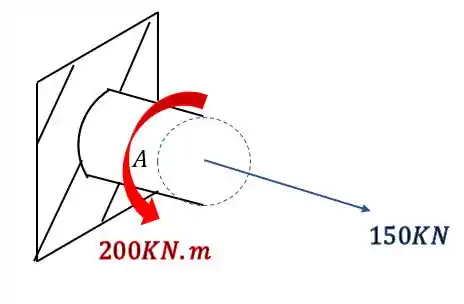
Mas da pra perceber que é difícil analisar os esforços em 3 dimensões, então pra facilitar podemos usar a regra da mão direita, em que os 4 dedos rodam na mesma direção dos momentos, e o polegar aponta na direção do vetor que usaremos pra representar, então nossa seção ficará
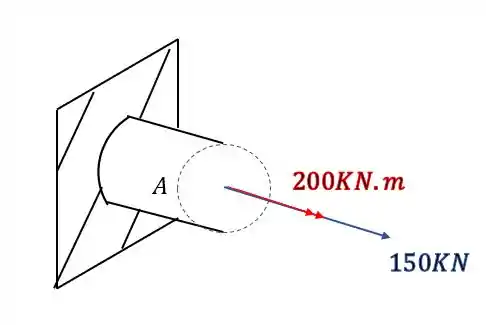
Passo 2
Agora que já descobrimos os esforços que aparecem, precisamos calcula-los. Já sabemos de antemão que a força normal produz esforços normais, e que o torsor produzem esforços de cisalhamento. Então vamos dividir essa segunda parte da solução em duas parte.
Primeiro vamos calcular os esforços normais devido a ação da força normal.
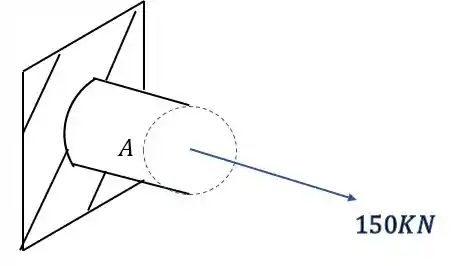
Sabemos que a fórmula que nos auxilia nesse cálculo é
Sabemos que o normal será dado por
E a área será dada por
Substituindo na fórmula principal teremos que
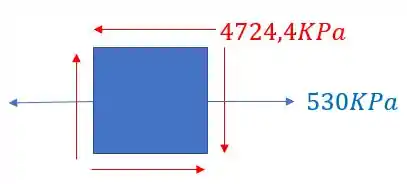
Olhando novamente a figura, vemos que nosso elemento é
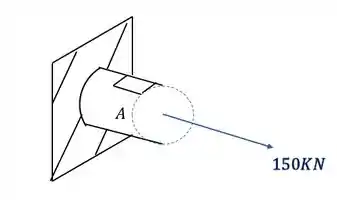

É importante perceber, que como calculamos o valor de tensão normal e ele deu positivo, significa que ele está tracionado o nosso elemento.
Passo 3
Por fim basta analisarmos os esforços para a ação do Torso.
Sabemos que a fórmula que nos dá isso é
Vamos ir deduzido cada valor da nossa fórmula.
Sabemos que o se trata do ponto que estamos calculando, como esse ponto está na extremidade, o valor será o próprio raio da seção
Também temos que determinar o nosso momento torsor
Pela figura temos que
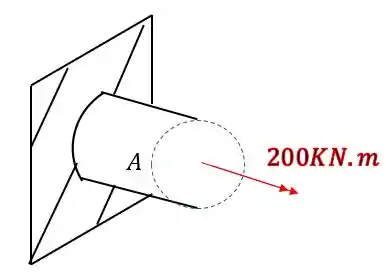
teremos que
Por fim falta o cálculo do J que é dado pela equação
Substituindo teremos que
Agora que já temos todos os valores
Vamos substituir na nossa equação principal
Mas como representamos isso no nosso elemento?
Basta apenas analisar o diagrama formado nessa figura
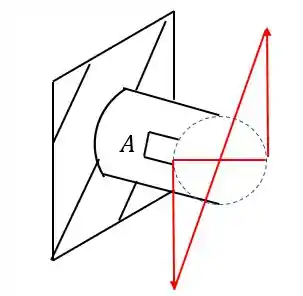
Logo a representação no nosso elemento será
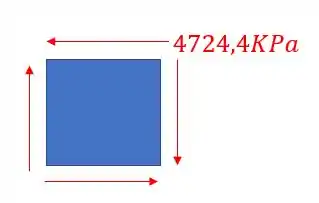
E pela convenção de sinais, quando as setas se concentram no segundo e no quarto quadrante teremos uma tensão negativa.
Passo 4
Por fim basta fazermos o elemento final com todos os esforços que representamos anteriormente, tendo dessa maneira o seguinte elemento para representarmos.