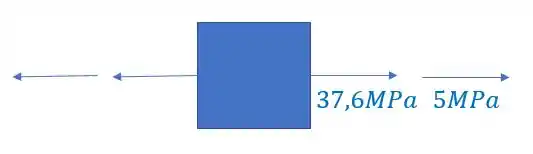
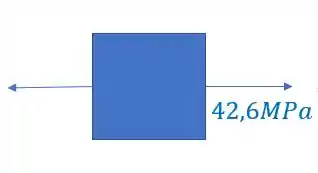
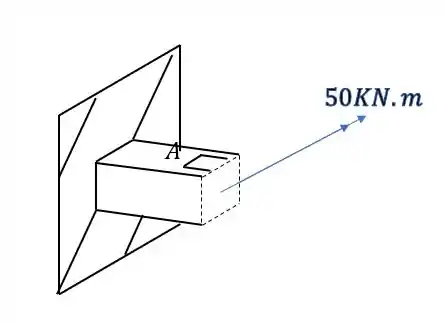
Uma barra esta sujeita a um esforço fletor e uma carga normal. Determine dessa forma o estado plano de tensões no ponto A da barra. Seção da barra (20x20cm).
Passo 1
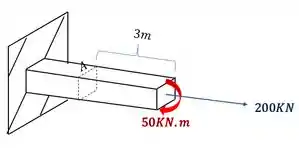
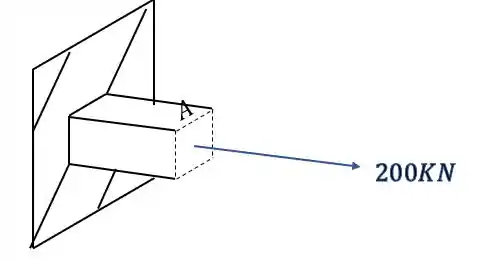
Nesse tipo de questão, é sempre bom tomar extremo cuidado com as contas feitas. É muito importante fazer cada parte tomando extremo cuidado. Primeiro devemos levar todos os esforços do extremo da barra para o ponto que desejamos calcular, o desenho abaixo representa como vamos fazer isso.
Primeiro olhamos a seção que temos que levar os esforços
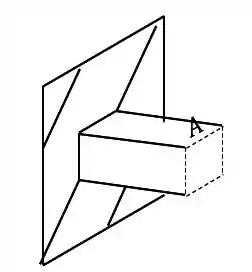
Em seguida analisamos quais solicitações os nossos esforços produziram
Sabemos que temos força Normal
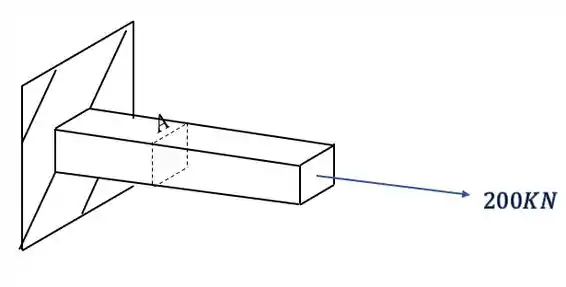
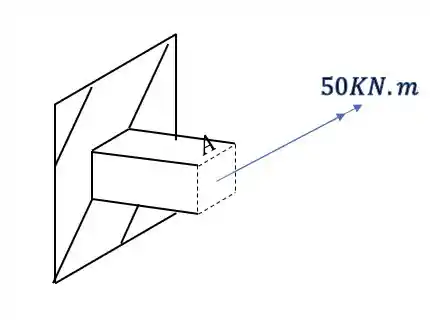
Sabemos que temos esforço fletor também
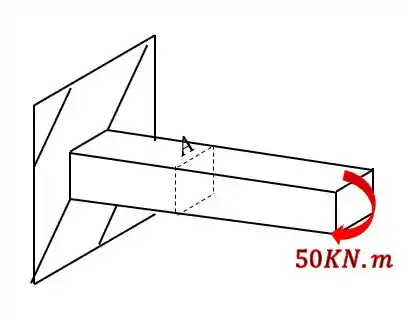
Levando todos esses esforços para nossa seção, teremos que
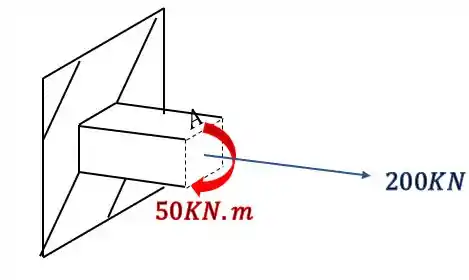
Mas da pra perceber que é difícil analisar os esforços em 3 dimensões, então pra facilitar podemos usar a regra da mão direita, em que os 4 dedos rodam na mesma direção dos momentos, e o polegar aponta na direção do vetor que usaremos pra representar, então nossa seção ficará
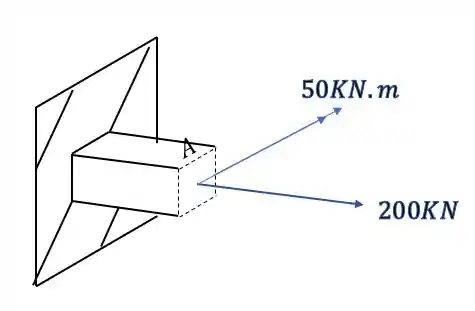
Passo 2
Agora que já descobrimos os esforços que aparecem, precisamos calcula-los. Já sabemos de antemão que a força normal produz esforços normais, assim como o momento fletor. Então vamos dividir essa segunda parte da solução em duas parte.
Primeiro vamos calcular os esforços normais devido a ação da força normal.
Sabemos que a fórmula que nos auxilia nesse cálculo é
Sabemos que o normal será dado por
E a área será dada por
Substituindo na fórmula principal teremos que
Olhando novamente a figura, vemos que nosso elemento é
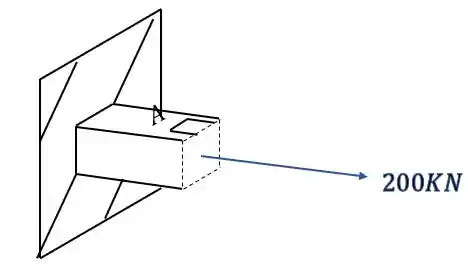
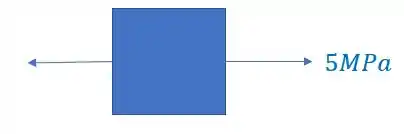
É importante perceber, que como calculamos o valor de tensão normal e ele deu positivo, significa que ele está tracionado o nosso elemento.
Passo 3
Vamos calcular os esforços normais devido a ação do momento fletor.
Sabemos que a fórmula que nos auxilia nesse cálculo é
Sabemos que y é a distância da linha neutra da peça até o ponto calculado, como esse ponto está em cima, sabemos que seu sinal é negativo, e por estar na extremidade, vale o próprio valor da metade do lado.
Também temos que calcular o valor do momento
Sabemos pela figura que o nosso momento fletor é
Por fim, basta determinar o valor do momento de inercia de uma barra quadrada, que é dada por
Substituindo os valores do enunciado teremos que
Substituindo na nossa equação teremos que
Olhando novamente a figura, vemos que nosso elemento é
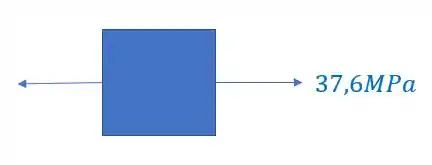
É importante perceber, que como calculamos o valor de tensão normal e ele deu positivo, significa que ele está tracionado o nosso elemento. Você também pode perceber isso fazendo a regra da mão direita no ponto A e vendo que ele é tracionado quando fazemos isso.
Passo 4
Por fim basta fazermos o elemento final com todos os esforços que representamos anteriormente, tendo dessa maneira o seguinte elemento para representarmos.