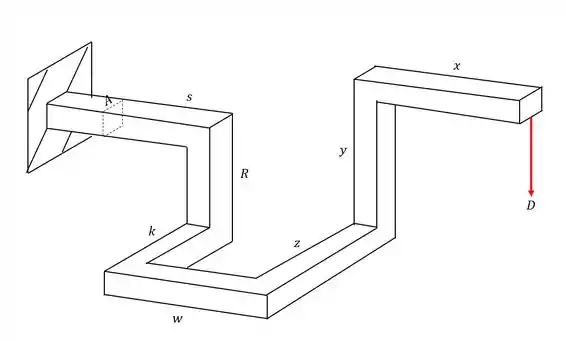
Quais forças iram contribuir para o cálculo dos esforços que agirão na seção da nossa peça no ponto A.
Observação: não precisa calcular os valores do estado de tensões, apenas indicar os esforços.
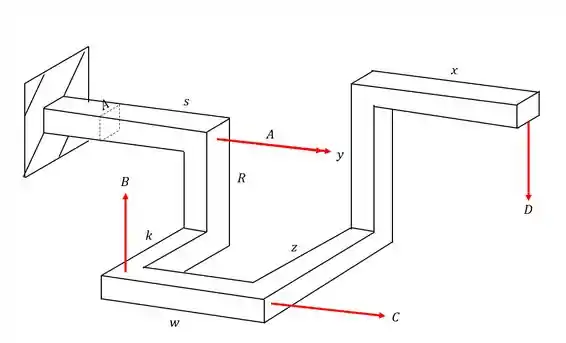
Passo 1
Para começar essa questão, devemos nos lembrar do nosso passo a passo. Devemos primeiro levar todos os esforços produzidos pelas cargas para a seção que se deseja calcular e analisar como esses esforços afetam o ponto A.
Analisando primeiro a carga de A vemos que ela produz uma tensão cisalhante pela ação do torsor, e sabemos que a fórmula para calcularmos a tensão em função do torsor é
Analisando a nossa seção teremos que
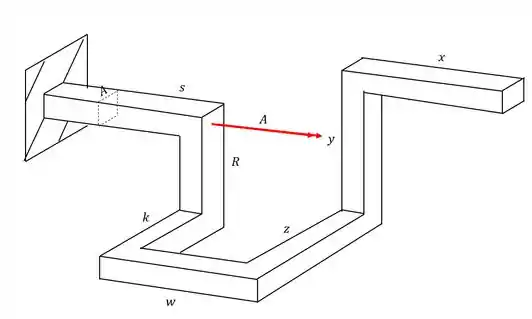
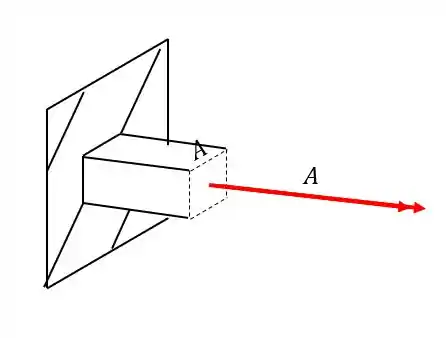
Como apenas se trata de um esforço de torção, basta que levemos diretamente para a nossa seção diretamente, sem nos preocuparmos com braços de alavanca por exemplo.
Passo 2
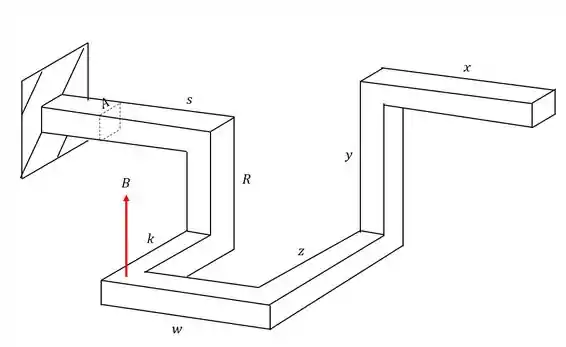
Analisando a carga B vemos que ela produz 3 esforços. O primeiro é o próprio esforço de cortante, que produz a tensão cisalhante, que usamos a fórmula
Também vemos que ele produz um esforço fletor, com braço de alavanca S, e que é calculado pela fórmula
Porém também vemos que ele produz um torsor com braço de alavanca K, e que será calculado pela fórmula
Olhando a nossa seção teremos que
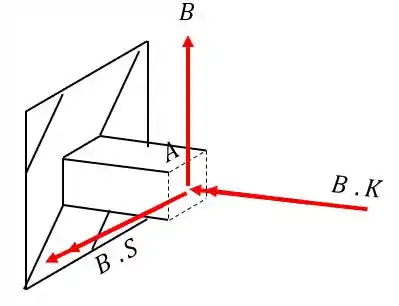
Passo 3
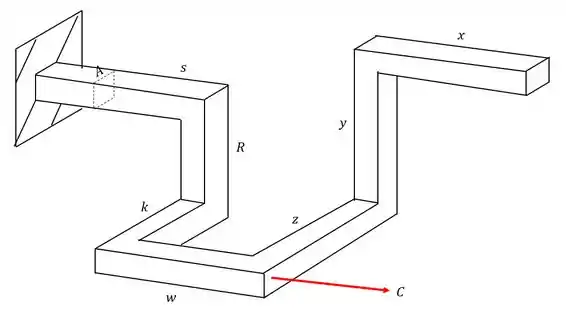
Analisando a carga C vemos que ela produz 3 esforços. O primeiro é o próprio esforço de tração, que usamos a fórmula
Também vemos que ele produz um esforço fletor, com braço de alavanca K, e que é calculado pela fórmula
Porém também vemos que ele produz um fletor com braço de alavanca R, e que será calculado pela fórmula
Olhando a nossa seção teremos que
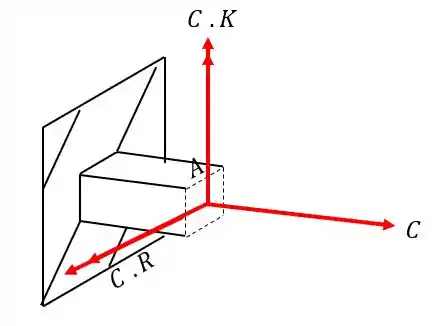
O ponto A está exatamente em cima da linha neutra causada pelo momento fletor , ou seja, a contribuição do momento fletor nesse caso é zero.
Passo 4
Analisando a carga D vemos que ela produz 3 esforços. O primeiro é o próprio esforço de cortante, que produz a tensão cisalhante, que usamos a fórmula
Também vemos que ele produz um esforço fletor, com braço de alavanca , e que é calculado pela fórmula
Porém também vemos que ele produz um torsor com braço de alavanca , e que será calculado pela fórmula
Olhando a nossa seção teremos que
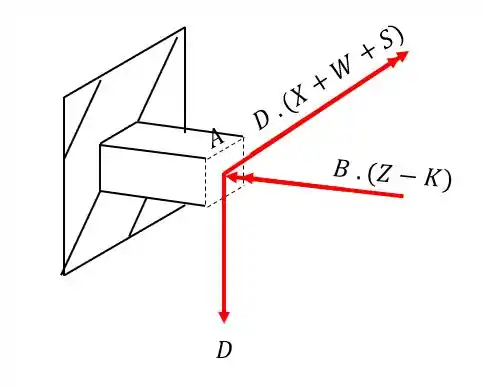
Passo 5
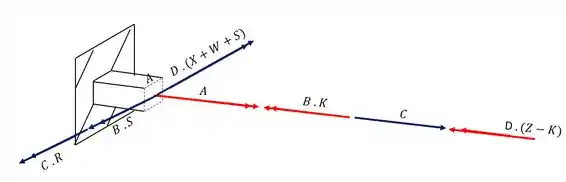
Analisando todos os esforços que agem na seção teremos que
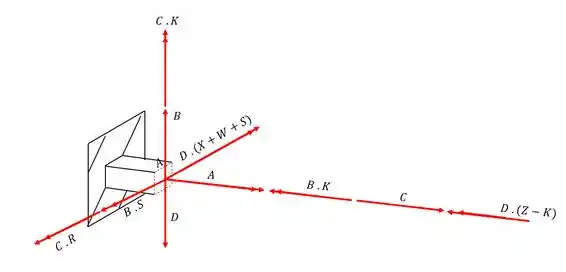
Como já vimos os momentos fletores que contém o ponto A não iram influenciar no nosso valor logo, os esforços que devemos considerar são
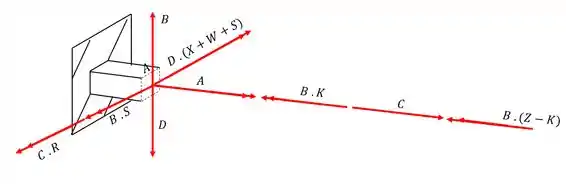
Outra coisa que podemos notar é, como o ponto A está na extremidade da seção, sabemos que o momento estático dele é zero, ou seja, a contribuição das tensões cisalhantes devido a ação do cortante também será zero, então teremos que
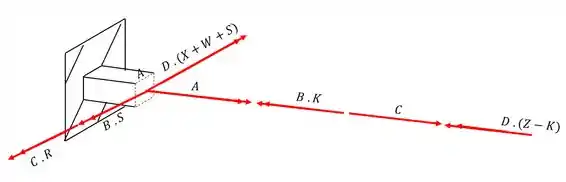
Dividindo em azul as tensões que causam esforço normal e de vermelho os esforços cisalhantes teremos que
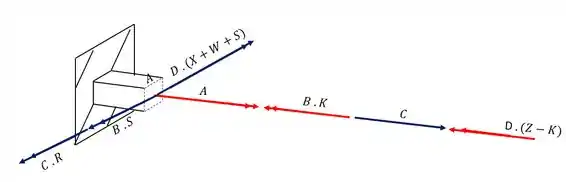
Resposta
Os esforços que contribuem são os que estão demonstrados na figura abaixo, exatamente na seção que destacamos, logo temos que