O eixo tem diâmetro e está sujeito às cargas mostradas. Faça um desenho do estado plano de tensões para um ponto na superfície desse eixo.

Passo 1
O que está acontecendo?
O eixo tem um diâmetro .
As forças axiais nele vão gerar em todas as seções dele uma força interna normal :
...uma vez que essas forças são forças de compressão.
Essa força interna normal por sua vez vai gerar em todos os pontos dessas seções uma tensão normal média .
Dessa forma, já sabemos que vai haver em um ponto na superfície desse eixo uma tensão normal média .
Além disso...
Os torques no eixo vão gerar nele torques internos (também conhecidos como momentos torsores dependendo dos seus professores):
Como mostra a análise dos esforços internos abaixo:
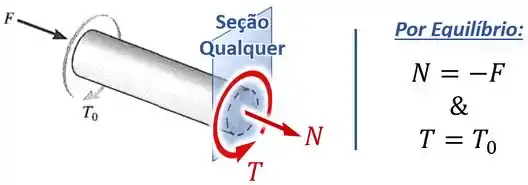
Esse torque interno , por sua, vez, vai gerar nos pontos dessa seção uma tensão de cisalhamento de acordo com a fórmula da torção:
Onde:
- é a distância do centro da seção até o ponto em que se quer saber a tensão ;
- & é o momento de inércia polar da seção e é dado pela fórmula:
...para uma seção circular de raio .
(No nosso caso, vamos usar , uma vez que o raio é a metade do diâmetro.)
E o que é que o exercício quer?
Ele quer que a gente desenhe o estado plano de tensões em um ponto na superfície desse eixo.
Para tanto, devemos escolher um ponto qualquer na superfície desse eixo, como um logo atrás da seção qualquer que fizemos, por exemplo:

Com isso, podemos agora estudar como são as tensões e nesse ponto.
Aí, conhecendo essas tensões, vamos poder desenhar os resultados em um elemento quadrado representando o ponto.
E aí esse desenho vai ser o estado plano de tensões pedido pelo exercício!
Passo 2
Então vamos lá!
Vamos começar calculando a tensão normal causada pela força normal .
Aplicando a fórmula da tensão normal média, temos:
Aí, substituindo:
- ;
- E a área da seção transversal circular de diâmetro , ,
Encontramos que:
O que significa que o nosso ponto é comprimido na horizontal (que é a direção da força normal ) por uma tensão normal de intensidade :
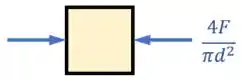
Ok!
Passo 3
Agora, vamos encontrar a tensão cisalhante causada pelo torque interno .
Aplicando a fórmula da torção, temos:
Aí, substituindo:
- ;
- & ,
...e percebendo que para um ponto na superfície do nosso eixo, a distância vai ser igual ao raio do eixo, vamos ter que:
Simplificando isso, temos:
Finalmente, substituindo , encontramos que a tensão de cisalhamento no nosso ponto é:
Por último, ainda precisamos entender qual vai ser a direção dessa tensão cisalhante .
Daí que, olhando para o sentido do torque interno e para o nosso ponto:

...vemos que a tensão cisalhante causada por vai apontar para baixo no lado direito desse ponto que escolhemos:
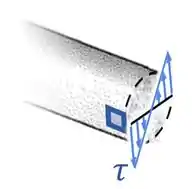
Aí, representando isso no nosso ponto, temos:
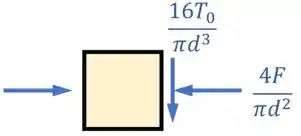
Por fim, para equilibrar essa tensão, temos que desenhar outras 3 tensões cisalhantes nos outros lados do elemento:
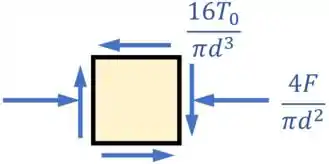
E pronto!
Esse desenho acima é o estado plano de tensões para um ponto na superfície desse eixo e é a nossa resposta para o exercício.