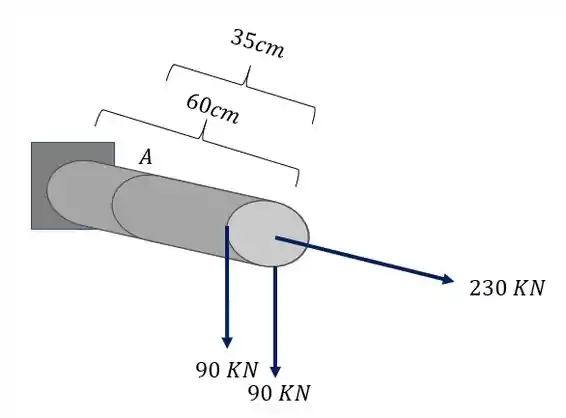
A barra de aço circular abaixo, de diâmetro 20mm, foi sujeita ao carregamento mostrado na figura. Determine o estado plano de tensões que ocorrem no ponto A da nossa barra.
Passo 1
Para começar essa questão, devemos nos lembrar do nosso passo a passo. Devemos primeiro levar todos os esforços produzidos pelas cargas para a seção que se deseja calcular e analisar como esses esforços afetam o ponto A.
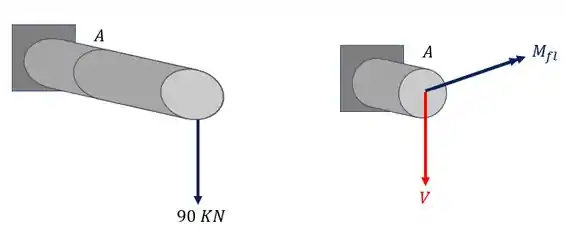
Analisando primeiro a carga de 90KN que está deslocada vemos que ela produz uma força cortante, um esforço torçor e também um esforço fletor como mostra a figura abaixo.
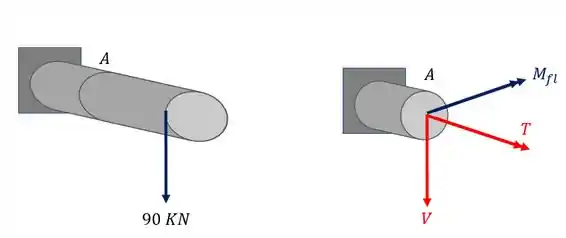
podemos ver também que a carga de 90 KN não deslocada produz na nossa seção uma componente cortante e também um momento fletor
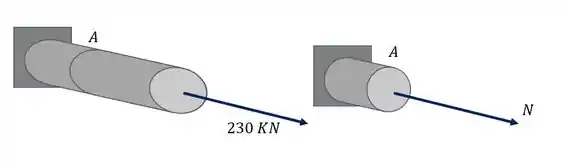
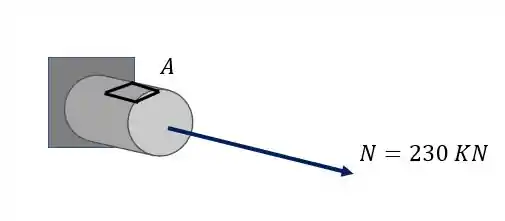
Além disso podemos ver que a carga de 230 KN não deslocada produz na nossa seção apenas uma componente, que nesse caso é uma força normal, como podemos ver na nossa figura
Analisando a nossa seção com todos os esforços juntos teremos que
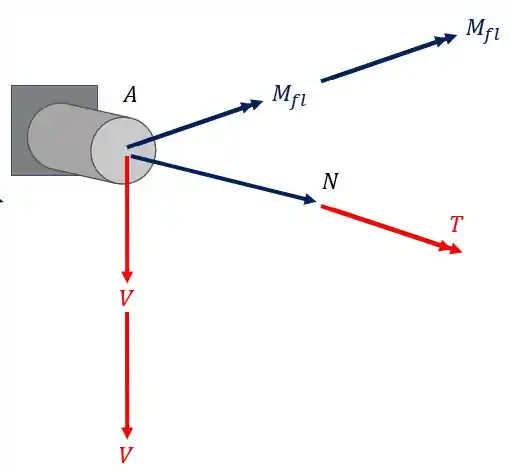
Nesse caso tanto o cortante quanto o momento fletor são iguais pois ambas as cargas são iguais e estão a mesma distância da nossa seção, logo não precisamos usar características diferentes já que ambos os valores são idênticos.
Passo 2
Agora que já descobrimos os esforços que aparecem, precisamos calcula-los. Já sabemos de antemão que a força normal produz esforços normais, assim como o momento fletor. Da mesma forma força cortante produz esforços cisalhantes assim como o torsor. Então vamos dividir essa segunda parte da solução em duas partes.
Primeiro vamos calcular os esforços normais devido a ação da força normal.
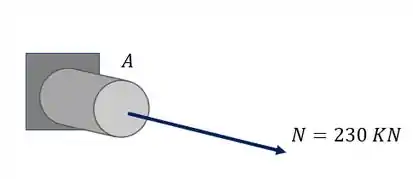
Sabemos que a fórmula que nos auxilia nesse cálculo é
Sabemos que o normal será dado por
E a área será dada por
Se o diâmetro é 20mm o raio será metade disso, ou seja, 10mm, então temos que
Substituindo na fórmula principal teremos que
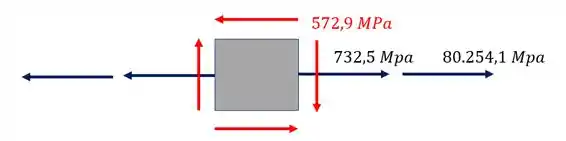
Olhando novamente a figura, vemos que nosso elemento é
O nosso elemento isolado com a tensão será
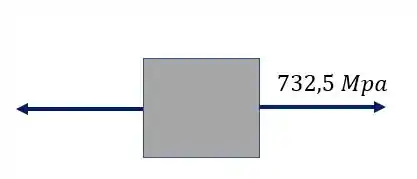
É importante perceber, que como calculamos o valor de tensão normal e ele deu positivo, significa que ele está tracionado o nosso elemento.
Passo 3
Vamos calcular os esforços normais devido a ação do momento fletor. Mas perceba o seguinte, como temos dois momentos fletores iguais, basta calcularmos apenas um dos momentos e multiplicar o valor por dois. Temos dois momentos fletores causados pela carga de 90 KN e ambas possuem o mesmo braço de alavanca, por isso ambos são iguais.
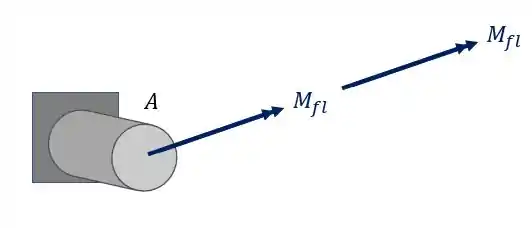
Sabemos que a fórmula que nos auxilia nesse cálculo é
Sabemos que y é a distância do centro da peça até o ponto calculado, como esse ponto está em cima, sabemos que seu sinal é positivo, e por estar na extremidade, vale o próprio valor raio.
Também temos que calcular o valor do momento
Sabemos pela figura que o nosso momento fletor é o braço de alavanca da carga de 90KN e o próprio valor do braço de alavanca, além é claro de ser negativo por ser contrario aos eixos adotados
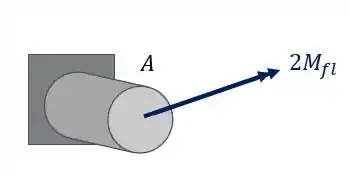
Como são dois momentos teremos que
Por fim, basta determinar o valor do momento de inercia de uma barra circular, que é dada por
Substituindo os valores do enunciado teremos que
Substituindo na nossa equação teremos que
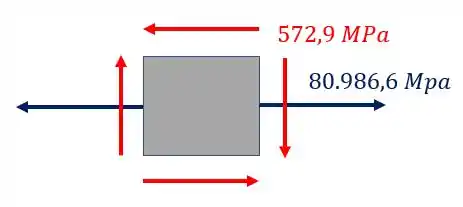
Olhando novamente a figura, vemos que nosso elemento é
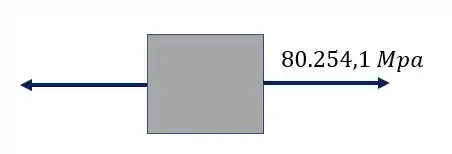
É importante perceber, que como calculamos o valor de tensão normal e ele deu positivo, significa que ele está tracionado o nosso elemento. Você também pode perceber isso fazendo a regra da mão direita no ponto A e vendo que ele é tracionado quando fazemos isso.
Passo 4
Agora vamos fazer a análise por esforços cisalhantes.
Vamos primeiro analisar o cisalhante. Sabemos que a fórmula que nos auxilia no cálculo é a f��rmula
Mas vamos olhar a nossa figura. Lembre-se que os nossos cortantes são iguais, assim teremos que
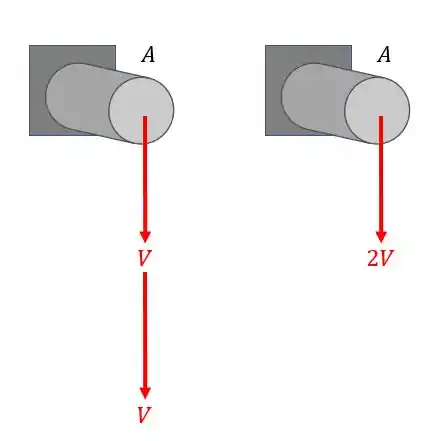
Queremos o cisalhante em A, então basta você pensar no seguinte, uma das coisas pedidas nessa conta é o momento estática(S), que é a área acima do ponto que calculamos o cisalhante.
Agora pensa comigo, qual a área acima do ponto A?
Isso mesmo, não tem, logo
Se o momento estático em A é zero, podemos deduzir que
Outra forma de calcular seria lembrando do nosso diagrama, que para esforço cortante é zero nas extremidades e máximo na linha neutra. Como aqui o ponto A está na extremidade, ele vale zero, para exemplificar podemos ver isso no diagrama abaixo.
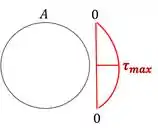
Passo 5
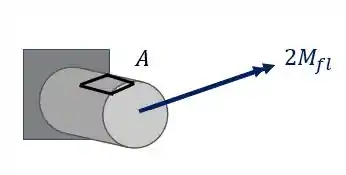
Por fim basta analisarmos os esforços para a ação do Torso.
Sabemos que a fórmula que nos dá isso é
Vamos ir deduzido cada valor da nossa fórmula.
Sabemos que o se trata do ponto que estamos calculando, como esse ponto está na extremidade, o valor será o próprio raio da seção
Também temos que determinar o nosso momento torsor
Pela figura temos que
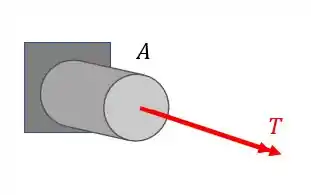

teremos que
Por fim falta o cálculo do J que é dado pela equação
Substituindo teremos que
Agora que já temos todos os valores
Vamos substituir na nossa equação principal
Mas como representamos isso no nosso elemento?
Basta apenas analisar o diagrama formado nessa figura
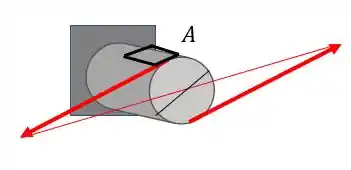
Logo a representação no nosso elemento será
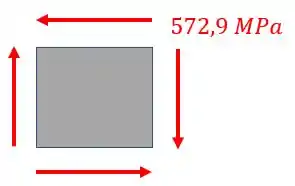
Passo 6
Por fim basta fazermos o elemento final com todos os esforços que representamos anteriormente, tendo dessa maneira o seguinte elemento para representarmos.