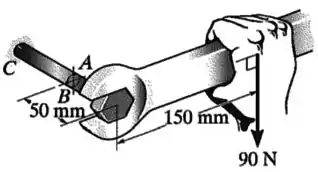
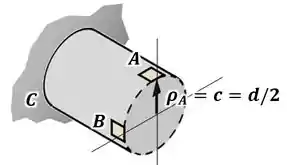
O parafuso está preso a seu suporte em . Se a força de for aplicada à chave para apertá-lo, determine as tensões normais e de cisalhamento no ponto . Além disso, represente os resultados sobre um elemento localizado nesse ponto. A haste tem diâmetro de .
Passo 1
O que está acontecendo?
A força de aplicada na chave vai gerar uma série de esforços internos na seção de diâmetro onde se encontram os pontos e .
Esses esforços internos, por sua vez, vão gerar tensões normais e tensões cisalhantes nesses pontos.
E o que é que o exercício quer?
Ele quer que a gente determine essas tensões e resultantes no ponto .
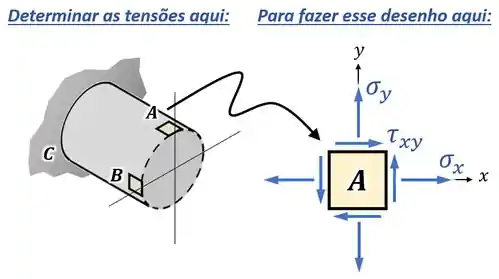
Em seguida, ele ainda quer que a gente represente esses resultados desenhando o estado plano de tensões para esse ponto, como ilustrado na imagem abaixo:
Então, para resolver esse exercício...
Devemos começar fazendo uma seção na peça no local onde está esse ponto .
Dessa forma, poderemos analisar e determinar os esforços internos que atuam nesse seção.
Com isso, vamos poder identificar as tensões e causadas por cada um desses esforços internos.
E, assim, vamos conseguir fazer os desenhos do estado plano de tensões para o ponto .
Passo 2
Então vamos começar fazendo uma análise dos esforços internos na seção onde se encontra o ponto .
Para tanto, podemos representar as peças de uma forma simplificada e fazer uma seção na região desse ponto:
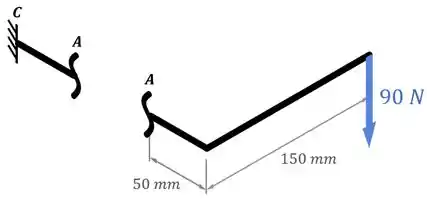
Feito isso, devemos identificar quais vão ser os esforços internos que vão surgir nessa seção.
Então lembra aí!
Os possíveis esforços internos são:
- Força normal ;
- Força cortante ;
- Momento fletor (ou );
- E torque interno (ou momento torsor ).
Desenhando esses esforços internos na nossa seção, o desenho acima fica assim:
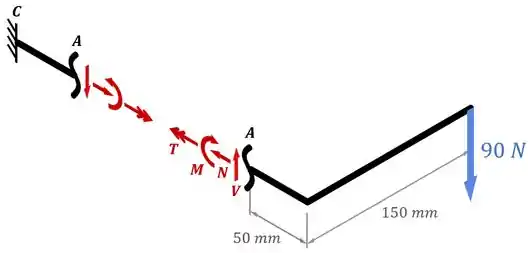
Lembrando que dependendo da convenção dos seus professores, o torque interno pode ser desenhado também entrando para dentro das peças.
Passo 3
Agora, precisamos calcular os valores desses esforços internos , , e .
Para tanto, podemos aplicar condições de equilíbrio para toda a parte direita das peças:
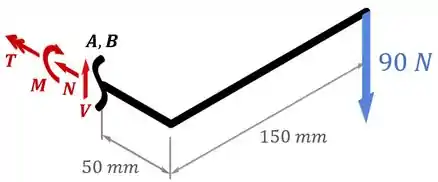
Primeiro, aplicando o equilíbrio de forças na horizontal, temos:
A única força na horizontal é a força normal , então temos que:
Ou seja, não há força normal nesse seção.
Em seguida, aplicando o equilíbrio de forças na vertical, temos:
Na vertical, temos a cortante para cima e a força de para baixo.
Dessa forma, esse somatório acima fica assim:
O que significa que:
Já para determinar o valor do momento fletor , precisamos aplicar o equilíbrio de momentos em relação ao ponto :
Em relação a esse ponto, nós vamos ter um momento no sentido horário () causado pela força de com um braço de e o momento também no sentido horário ().
Dessa forma, esse somatório de momentos acima fica assim:
O que significa que:
O que dá:
Por fim, para determinar o valor do torque interno , precisamos fazer um equilíbrio de torques:
Em relação ao eixo principal do parafuso, nós vamos ter um torque no sentido horário () causado pela força de com um braço de , além do próprio torque interno , também no sentido horário ().
Então o nosso somatório de torques fica assim:
O que significa que:
Passo 4
Agora que conhecemos os esforços internos na seção do ponto :
...podemos calcular as tensões causadas por esses esforços internos.
Nesse passo, vamos começar analisando a tensão de cisalhamento causada pela força cortante .
Lembra aí!
Ela é dada pela fórmula do cisalhamento:
Onde:
- é o momento estático para a fibra em que se quer calcular a tensão ;
- é o momento de inércia da área da seção transversal;
- & é a espessura da fibra em que se quer calcular a tensão .
Aí, se a gente olhar para o nosso ponto , vamos perceber uma coisa:
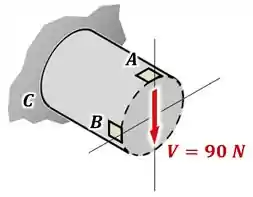
Que é: esse nosso ponto está no topo da seção!
E lá quando estudamos a fórmula do cisalhamento, vimos que o momento estático das fibras no topo e na base de uma seção é nulo.
Consequentemente, a tensão de cisalhamento devido à força cortante nos pontos dessas fibras é nula.
Ou seja:
A força cortante não vai causar nenhuma tensão no nosso ponto .
Passo 5
Em seguida, vamos ver como é a tensão causada pelo momento fletor no nosso ponto .
Lá quando estudamos flexão, vimos que a tensão normal causada por um momento fletor é dada pela fórmula da flexão:
Onde:
- é a posição do ponto em que se quer saber a tensão em relação à linha neutra;
- & é o momento de inércia da área da seção transversal.
No caso da nossa seção circular, temos que a linha neutra passa bem no meio dela:
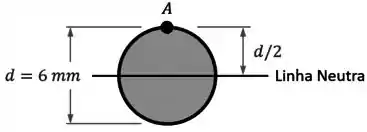
Aí, da imagem acima, vemos como a posição do nosso ponto é:
Além disso, para uma seção circular, o momento de inércia da área é dado pela fórmula:
Onde é o raio da seção e é igual à metade do diâmetro dela (), de tal forma que:
Sabendo de tudo isso, já podemos aplicar a fórmula da flexão para o nosso ponto :
Aí, substituindo:
- ;
- & ,
Temos que:
Simplificando, isso dá:
Finalmente, substituindo os valores:
- ;
- & ,
Encontramos que:
Calculando tudo isso, vamos ter um resultado em que vai dar:
Mas é o mesmo que , o que significa que:
E o que é que esse resultado significa?
Ele significa que o nosso ponto está sendo tracionado lateralmente por uma tensão normal de :
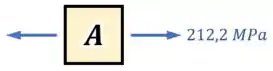
Passo 6
Por fim, podemos ver como será a tensão causada pelo torque interno .
Pelo que vimos lá em torção, sabemos que esse torque interno vai gerar na seção tensões de cisalhamento de acordo com a fórmula da torção:
Onde:
- é a distância do centro da seção até o ponto em que se quer saber a tensão ;
- & é o momento de inércia polar da seção e é dado pela fórmula:
...para uma seção circular de raio .
No nosso caso, vamos usar , uma vez que o raio é a metade do diâmetro, de tal forma que:
Aí, para o nosso ponto , a distância dele ao centro é igual ao raio da seção:
Assim, já podemos aplicar a fórmula da torção para o nosso ponto :
Substituindo:
- ;
- & ,
Temos:
Simplificando, temos:
Finalmente, substituindo os valores:
- ;
- & ,
Encontramos que:
Calculando tudo, e vendo que o resultando dessa equação vai sair em , que é o mesmo que , obtemos que:
Passo 7
Estamos quase terminando o exercício, mas ainda temos um último desafio que é saber em que sentido atua essa tensão de cisalhamento que acabamos de encontrar.
Isso porque:
- Enquanto que a fórmula da flexão é “inteligente” (ela consegue através do seu sinal de positivo ou negativo indicar se é uma tensão de tração ou compressão),
- A fórmula da torção não é “inteligente”.
Então nós temos que olhar pros desenhos que fizemos para entender qual é o sentido da tensão .
Podemos, por exemplo, olhar pro lado esquerdo do desenho que fizemos lá no começo do exercício:
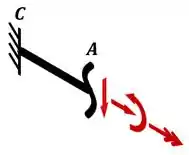
Nesse desenho, a seta dupla corresponde ao torque.
Visualizando esse torque na nossa peça com o auxílio da regra da mão direita, ele fica assim:
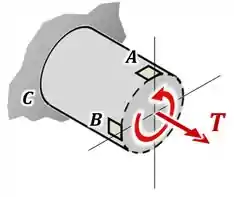
O que significa que caso ele fosse positivo, ele geraria uma tensão que apontaria para baixo no lado direito do ponto :
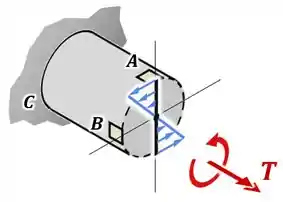
Mas na realidade, o torque interno e a tensão que encontramos tem valores negativos.
Isso significa que a tensão cisalhante de intensidade no nosso ponto vai na realidade estar apontando para cima no lado direito do ponto :
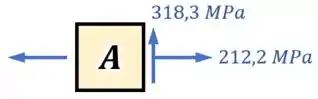
Por fim, para equilibrar esse elemento , devemos adicionar três outras tensões de cisalhamento com a mesma intensidade nos demais lados do elemento:
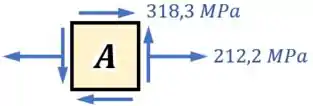
E pronto!
Esse desenho acima é o nosso estado plano de tensões para o ponto e completa nossa resposta para o exercício.
Além disso, na hora de destacar os valores das tensões no ponto para a resposta do exercício, podemos fornecer os valores de acordo com o caso geral do estado plano de tensões:
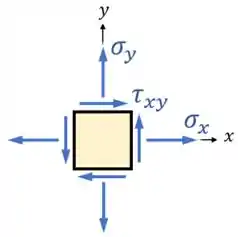
Comparando essa imagem com o nosso desenho acima, vemos que para o ponto :