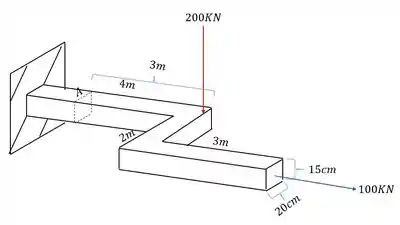
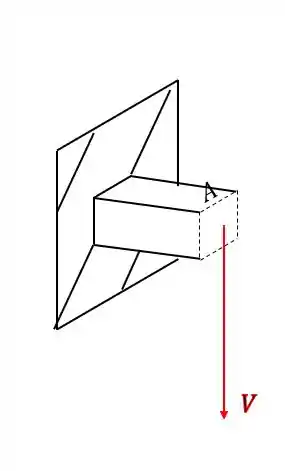
O pórtico abaixo está sujeito aos esforços mostrados. Dessa forma, determine o estado plano de tensões que age no ponto A desse pórtico.
Passo 1
Para começar essa questão, devemos nos lembrar do nosso passo a passo. Devemos primeiro levar todos os esforços produzidos pelas cargas para a seção que se deseja calcular e analisar como esses esforços afetam o ponto A.
Analisando primeiro a carga de 100KN vemos que ela produz uma força normal, e também um esforço fletor como mostra a figura abaixo.
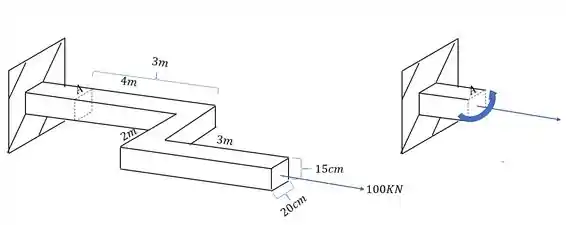
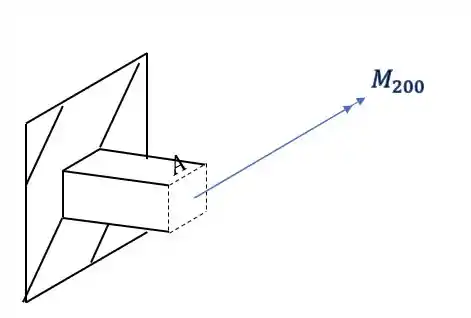
podemos ver também que a carga de 200KN produz na nossa seção uma componente cisalhante, e também um esforço fletor como mostrado na figura abaixo
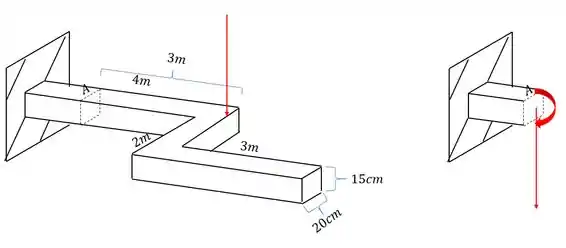
O que podemos perceber é que seria muito complexo analisar a figura com os esforços em 3 dimensões, então vamos facilitar e usar a regra da mão direita para colocarmos no lugar dos vetores momentos, os vetores que ficam na direção do nosso dedão. Fazendo isso teremos que o nosso elemento ficará
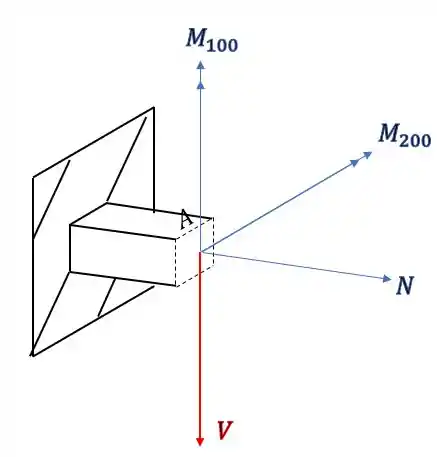
Passo 2
Agora que já descobrimos os esforços que aparecem, precisamos calcula-los. Já sabemos de antemão que a força normal produz esforços normais, assim como o momento fletor. Da mesma forma força cortante produz esforços cisalhantes. Então vamos dividir essa segunda parte da solução em duas parte.
Primeiro vamos calcular os esforços normais devido a ação da força normal.
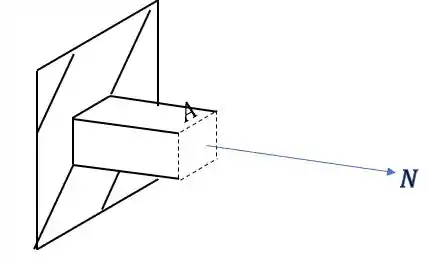
Sabemos que a fórmula que nos auxilia nesse cálculo é
Sabemos que o normal será dado por
E a área será dada por
Substituindo na fórmula principal teremos que
Olhando novamente a figura, vemos que nosso elemento é
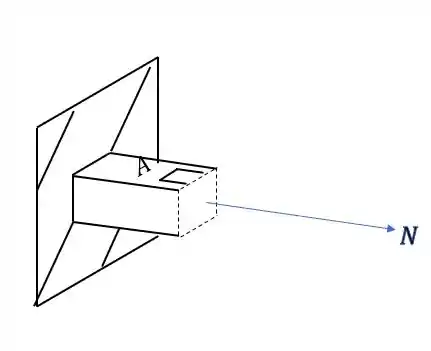
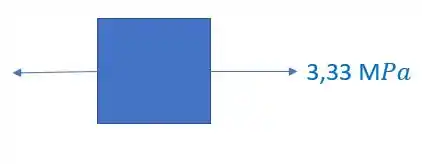
É importante perceber, que como calculamos o valor de tensão normal e ele deu positivo, significa que ele está tracionado o nosso elemento.
Passo 3
Vamos calcular os esforços normais devido a ação do momento fletor devido a carga de 200KN.
Sabemos que a fórmula que nos auxilia nesse cálculo é
Sabemos que y é a distância do centro da peça até o ponto calculado, como esse ponto está em cima, sabemos que seu sinal é positivo, e por estar na extremidade, vale o próprio valor da metade do lado.
Também temos que calcular o valor do momento
Sabemos pela figura que o nosso momento fletor é o braço de alavanca da carga de 200KN e o próprio valor do braço de alavanca, e é negativo pois é contrario ao sistema de eixos que adotamos.
Por fim, basta determinar o valor do momento de inercia de uma barra retangular, que é dada por
Substituindo os valores do enunciado teremos que
Substituindo na nossa equação teremos que
Olhando novamente a figura, vemos que nosso elemento é
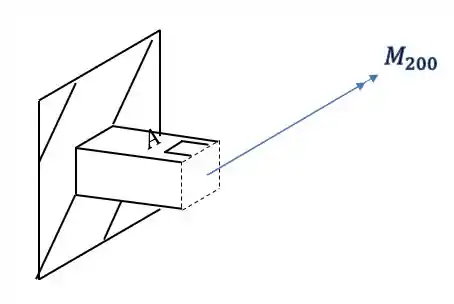
É importante perceber, que como calculamos o valor de tensão normal e ele deu positivo, significa que ele está tracionado o nosso elemento. Você também pode perceber isso fazendo a regra da mão direita no ponto A e vendo que ele é tracionado quando fazemos isso.
Passo 4
Vamos calcular os esforços normais devido a ação do momento fletor da carga de 100.
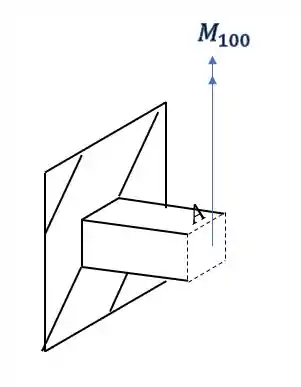
Sabemos que a fórmula que nos auxilia nesse cálculo é
Sabemos que y é a distância da linha neutra da peça até o ponto calculado, como esse ponto está na linha neutra, sabemos que seu valor é zero
Isso acontece porque, como o vetor momento está apontando na vertical, a linha neutra também estará na vertical. Basta utilizarmos a regra da mão direita e vamos perceber que o eixo de rotação nesse caso vai estar na vertical, com o ponto A logo em cima dele.
Se temos y=0 então substituindo só esse valor na fórmula principal teremos que
Logo o momento fletor produzido pela carga de 100KN não interfere no funcionamento do elemento do estado plano de tensões.
Aqui vale ressaltar que para momentos fletores máximos devemos fazer os cálculos para os pontos nas extremidades da peça, enquanto que o valor do momento sobre a linha neutra é zero.
Passo 5
Agora vamos fazer a análise por esforços cisalhantes.
Vamos primeiro analisar o cisalhante. Sabemos que a fórmula que nos auxilia no cálculo é a fórmula
Mas vamos olhar a nossa figura
Queremos o cisalhante em A, então basta você pensar no seguinte, uma das coisas pedidas nessa conta é o momento estática(S), que é a área acima do ponto que calculamos o cisalhante.
Agora pensa comigo, qual a área acima do ponto A?
Isso mesmo, não tem, logo
Se o momento estático em A é zero, podemos deduzir que
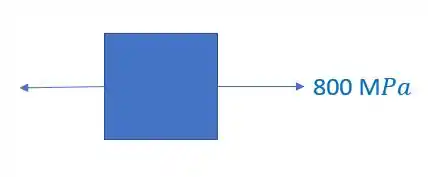
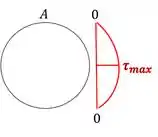
Outra forma de calcular seria lembrando do nosso diagrama, que para esforço cortante é zero nas extremidades e máximo na linha neutra. Como aqui o ponto A está na extremidade, ele vale zero, para exemplificar podemos ver isso no diagrama abaixo.
Passo 6
Por fim basta fazermos o elemento final com todos os esforços que representamos anteriormente, tendo dessa maneira o seguinte elemento para representarmos.