(Adaptada) Considere um cone circular reto uniforme de densidade , flutuando com seu vértice para baixo na água (). O raio da base é e a altura do cone é . Calcule e verifique se esse cone é estável para a altura submersa .
Dados: e .
Passo 1
Temos um cone flutuando e ele está invertido:
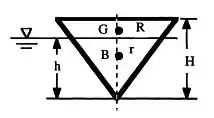
Para calcular GM:
Vamos começar analisando o centro de gravidade e calculando . Como o corpo é um cone, o centro de gravidade não é na metade da altura. Esse detalhe é muito importante! O centro de gravidade de um cone fica em um quarto da altura do mesmo.
Maaaas, como o cone está invertido (de cabeça pra baixo), então o centro de gravidade é representado por ¾ da altura do cone:
Do enunciado, sabemos que H = 1,2 m:
Passo 2
Para calcular vamos usar essa mesma lógica. A parte que está submersa também um cone, só que ao invés de raio R e altura H, o raio é r, e a altura h. Então, o ponto em que o empuxo será aplicado também será ¾ da altura do cone invertido:
Do enunciado, sabemos que h = 0,8 H:
Daqui podemos encontrar mais informações. Como sabemos que o corpo está em equilíbrio:
Ou seja:
Lembrando de geometria, o volume do cone é
E como o volume submerso é o volume de um cone também:
Substituindo:
Pelo enunciado, sabemos que:
Substituindo:
Vamos guardar essa expressão
Passo 3
Para calcular esse :
O momento de inércia será o momento de inércia do círculo, pois essa é a área tocada pelo fluido na superfície.
Lembrando que:
Substituindo e
Como e :
Passo 4
Agora, vamos calcular GM
Encontramos GM e é maior que zero! Logo, o cone é estável para h = 0,8 H 😊
Resposta
Estável