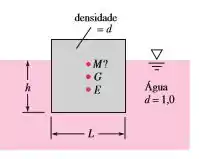
Um iceberg pode ser idealizado como um cubo de lado , como na Figura abaixo. Se a água do mar for representada por , então o gelo da geleira (que forma os icebergs) tem . Determine se esse iceberg “cúbico” é estável para a posição mostrada na Figura abaixo:
Passo 1
Vimos na teoria que o corpo flutuante estará estável se o for maior que zero.
A fórmula para calcular é:
Então para dizermos se o cubo está ou não estável devemos encontrar a posição do centro de carena, a posição do centro de gravidade e calcular o valor de .
O mais fácil de achar é a posição do centro de gravidade que é na metade do cubo, sendo assim:
Passo 2
Agora, vamos encontrar o :
Para isso precisamos saber qual o volume submerso e descobriremos isso usando o fato do sistema estar em equilíbrio. Assim,
O volume do cubo é e o volume submerso será
O centro de carena é esta na metade do volume submerso, sendo assim:
Passo 3
Agora só falta calcular o , que vimos uma fórmula para isso:
O momento de inércia do cubo é:
Passo 4
Substituindo os valores de que encontramos, temos:
Encontramos um positivo, mostrando que esse iceberg é estável.
Resposta
Estável