Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Estabilidade

Ver Teoria
Exercício 81234567

Enunciado

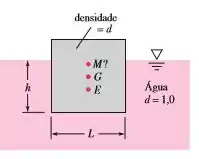
A idealização do iceberg do problema anterior (cubo de lado L parcialmente imerso na água do mar) pode se tornar instável se seus lados derreterem e sua altura exceder sua largura. Na Figura considere que a altura seja L e a profundidade normal ao papel seja L, mas a largura no plano do papel seja H   <   L . Considerando d   =   0,88 para o iceberg, encontre a razão H / L para a qual ele se torna neutramente estável (isto é, prestes a emborcar).

Passo 1

Nesse exercício, queremos achar a razão entre a altura e a largura do iceberg para que ele fique numa condição de equilíbrio indiferente (isso é o significa neutramente estável!)

Na teoria vimos que o equilíbrio indiferente é representado por G M   =   0 . Ou seja, o metacentro (M) coincide o centro de gravidade do iceberg (G)

Então, já temos essa equação aqui:

G M = K B - K G + B M

K B - K G + B M = 0

Então, a partir dos dados que temos do enunciado, vamos encontrar cada parcela dessa equação.

O mais simples de calcular é o centro de gravidade, então vamos começar por ele. Pelo enunciado, a altura desse iceberg é L. Considerando que o material é o gelo e ele é uniforme, então, o centro de gravidade do icerberg é:

K G = L 2

Passo 2

O segundo passo desse exercício é encontrar onde o empuxo está atuando! Assim, vamos conseguir calcular K B .

Como se trata de empuxo, precisamos saber qual é o volume submerso. Como o sistema está em equilíbrio (é o equilíbrio indiferente, mas ainda assim está em equilíbrio!) e as únicas forças atuantes são a força peso e o empuxo, então:

P = E

E pelas definições de cada um:

m g e l o . g = ρ á g u a . V s u b m e r s o . g

ρ g e l o . V i c e b e r g . g = ρ á g u a . V s u b m e r s o . g

Cortando a gravidade:

ρ g e l o . V i c e b e r g = ρ á g u a . V s u b m e r s o

O volume do iceberg é

V i c e b e r g = a l t u r a   × l a r g u r a × p r o f u n d i d a d e

V i c e b e r g = L   × H × L

V i c e b e r g = L 2   × H

E o volume submerso será

V s u b m e r s o = h × H × L

Substituindo:

ρ g e l o . V i c e b e r g = ρ á g u a . V s u b m e r s o

0,88 . L 2 . H = 1 . h . H . L

0,88 . L = 1 . h

h = 0,88 L

O ponto de atuação do empuxo é no centro de gravidade da parte submersa:

K B = h 2

Substituindo a expressão de h

K B = 0,88 . L 2

Passo 3

Atualizando a equação do Passo 1:

K B - K G + B M = 0

0,88 . L 2 - L 2 + B M = 0

Falta calcular esse B M . Temos uma fórmula para ele! YAY!

B M = I 0 V s u b m e r s o

O momento de inércia do iceberg é:

I 0 = p r o f u n d i d a d e × l a r g u r a 3 12

Pelo enunciado:

I 0 = L . H 3 12

B M = L . H 3 12   h . H . L = H 2 12.0,88 . L

B M = H 2 10,56 . L

Vamos guardar isso aí!

Passo 4

Opa, agora vamos atualizar finalmente a equação com os valores encontrados. :D

K B - K G + B M = 0

0,88 . L 2 - L 2 + H 2 10,56 . L = 0

Multiplicando por 2 L

0,88 . L 2 - L 2 + 2 H 2 10,56 = 0

2 H 2 10,56 = L 2 - 0,88 . L 2

2 H 2 10,56 = 1 - 0,88 . L 2

Isolando H/L:

H 2 L 2 = 10,56 . ( 1 - 0,88 ) 2

Logo:

H L = 10,56 . ( 1 - 0,88 ) 2

H L =     0,796

Show! Então para que o iceberg esteja em equilíbrio indiferente, a razão entre largura e profundidade deve ser 0,796!

Resposta

H L =     0,796

Exercícios de Livros Relacionados

Um objeto de madeira é mostrado na figura. O seu peso é 2,5N e o centro de gravidade está a 5c m da superfície superior. O equilíbrio é estável em relação ao eixo y ?
Um cubo de peso específico γ c flutua num líquido de peso específico γ l . Determinar a relação γ c / γ l para que o cubo flutue com as arestas na vertical.
Qual a máxima altura H de um cilindro de seção circular de raio R , para que possa flutuar em equilíbrio estável com seu eixo na vertical em qualquer líquido? Dados: cilindro γ ; líquido γ l .
Considere um cilindro de densidade d1 flutuando verticalmente na água ( d = 1 ) , como na Figura P2.127. Deduza uma fórmula para os valores estáveis de D / L em função de d e aplique-a ao caso D / L =
Considere que o balão do Problema P2.111 seja construído para ter um diâmetro de 14m , cheio ao nível do mar com ar quente a 70 ℃ ℃ e 1a t m , e seja liberado. Se o ar dentro do balão permanecer const