Ao flutuar em água , um corpo triangular equilateral pode assumir uma das duas posições mostradas na Figura abaixo. Qual é a posição mais estável? Considere que a largura seja grande normal ao papel.
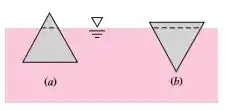
Passo 1
Para resolvermos essa questão existem algumas informações que devemos saber sobre um triangulo equilátero.
Possui os três lados iguais e a altura do triângulo é a área é .
O centro de gravidade de um triângulo é em relação a base.
Beleza agora pode começar a pensar no problema, para sabermos quem é mais estável devemos ver qual caso possui o maior .
Caso
A posição do centro de gravidade é , nesse caso então:
Agora temos que achar a posição do centro de empuxo, para isso vamos usar do fato de estarmos em equilíbrio e peso ser igual a empuxo. Assim,
Para calcular o volume dessa peça, vamos fazer a área do triangulo e multiplicar pelo comprimento que é muito grande. Assim, temos:
A área submersa é a área do triangulo equilátero, menos a área de um mini triangulo equiláteros de lado .
Então, temos:
Cortando o que conseguimos temos:
A altura desse pequeno triangulo equilátero é:
Assim a altura da parte submersa é:
Agora precisamos encontrar o centro geométrico do trapézio submerso. Para isso vamos ter que usar uma antiga fórmula que usávamos para calcular centro de área de figuras com furos.
Pois iremos imaginar que o trapézio é o triangulo grande menos o triangulo pequeno. Assim o centro geométrico da figura submersa será:
Já lhes peço desculpas, mas agora vem uma parte cheia de letras e algebrismo que de física não tem nada.
Cortando e substituindo o , chegamos em:
Ufaa, acabou! Podemos voltar a parte importante da questão agora.
Tendo e , falta apenas encontrar para calcularmos .
Lembre-se que o momento de inércia é de onde o fluido corta o objeto, sendo assim, o momento de inércia da nossa figura, será:
O volume submerso, já calculamos e vale:
Sendo assim, é:
O dessa posição é:
Sendo assim esse primeiro caso é instável.
Passo 2
Agora vamos analisar o caso :
Nesse caso o centro de gravidade está localizado a
Agora, para encontrar o centro de empuxo, temos que usar
O volume submerso, será a largura vezes a área de um triangulo equilátero de lado .
Assim, a posição do centro de carena é:
A altura do triangulo de lado é:
Então:
Por fim falta apenas calcular o , para isso precisamos saber o momento de inércia da linha do fluido.
Assim,
Agora temos tudo que é necessário para calcular o ,
O dessa posição é maior que zero, assim maior que o da posição sendo assim a posição mais estável.
Resposta
Caso é o mais estável.